Basic information of Statistics
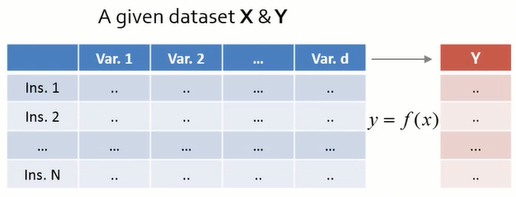
이번 글에서는 통계학에서 기본적으로 사용되는 용어, 개념들을 정리하였다. Sample space (표본공간) : The sample space $S$ is a set that contains all possible experimental outcomes. Experiment (실험) : Any process for which more than one outcome is possible. (Any process that generates data) Event (사건) : A subset of the sample space $S$ Random variable : A function that assigns real number to each element of sample space. $$Real\;numbers = f(Elements\;of\;the\;sample\;space)$$ 확률 변수의 종류 1. Discrete random variables (이산확률변수) : Outputs of a random variable are finite discrete (countable) values. (0, 1, 2, ...) 2. Continuous random variables (연속확률변수) : Outputs of a random variable are continuous (uncountable) values. Probability function ($f$) $$p = f(x)$$ $$x\;:\;Real\;numbers\;that\;the\;Random\;variables\;can\;take$$ $$0 \leq p \leq 1$$ $x$가 이산확률변수이면, $f$는 Probability mass function (p.m.f. : 확률질량함수) 이고 $x$가 연속확률변수이면, $f$는 Probability density function (p.d.f. : 확률밀도함수) 이다. Probability mass function (pmf : 확률 질량 함수) For a discr...