XGBoost : A Scalable Tree Boosting System
04_7 : Ensemble Learning : XGBoost : A Scalable Tree Boosting System
이 글은 XGBoost를 공부하면서 이해한 내용들을 정리한 글이다. 논문에는 생략되어있는 수식 전개를 나름 쉽게 설명해보려 하다보니 내용도 많고 수식도 많다. 정리하는데 너무 힘들었다ㅠㅜ 각 항목별로 논문의 몇번째 항목인지 부제목 옆에 적어놓았으니, 글을 읽을 때 논문을 함께 보도록 하자! (논문)
XGBoost는 기존 Gradient Boosting 방법에 Approximation 방법을 적용하여 Parallelize를 가능하게 하고, 하드웨어적인 최적화를 하여 더 빠르게 학습을 진행하면서 동시에 좋은 성능을 보인다.
XGBoost가 각광받은 이유 중 하나는 Scalability(확장성)이다. 여러 종류의 데이터들과 목적에 잘 적용되고, 빠르고, 좋은 성능을 보인다.
우선 앞서 다른 글에서 이야기 했었지만, 다시한번 기본적인 Ensemble : Tree Boosting 방법에 대하여 짚고 넘어가자.
Regularized Learning Objective (Article 2.1)
주어진 Dataset이 $n$개의 example(instance)들과 $m$개의 feature(variable)로 이루어져 있다고 가정하자. 그렇다면 Ensemble model의 추정값은 아래와 같다.
$$\hat{y}_i = \phi (x_i) = \sum_{k=1}^K f_k(x_i),\;\;\;\;\;\;f_k \in \mathcal{F}$$
$$where\;\;\mathcal{F} = \{f(x) = w_{q(x)}\}\;\;(q:\mathbb{R}^m \rightarrow T,\;w\in \mathbb{R}^T)$$
$\mathcal{F}$는 모든 가능한 함수들을 포함하는 Function space이고, 함수 $f_k$는 각각의 Classification and regression tree(CART)이다. CART에서는 각 data들을 $q(x)$에 따라 분류하고, 분류된 data에 해당 leaf node의 값 (weight)를 해당 data의 예측값으로 사용하였다.
AdaBoost의 경우에는 이전 base learner $f_{k-1}$를 기반으로 다음 base learner $f_{k}$가 학습할 data set의 선택기준 weight를 조절하였고, GBM의 경우에는 다음 base learner $f_{k}$가 이전 base learner $f_{k-1}$가 예측하지 못한 residual을 예측하도록 하였다.
CART를 다시 살펴보자. CART에 대하여 적절한 $w$와 $q$를 어떻게 선택하게 하고, 얼마나 좋은지 어떻게 판단할까? 앞서 공부했듯이 Loss function $l$을 사용한다. 우리의 목적은 아래 Objective function $\mathcal{L}$을 최소화 하는 것이다.
$$\mathcal{L}(\phi) = \sum_i l(y_i,\hat{y}_i) + \sum_k \Omega (f_k)$$
$$where\;\;\Omega(f) = \gamma T + \frac{1}{2} \lambda ||w||^2$$
$\sum_i l(\hat{y}_i,y_i)$이 부분이 각 CART들의 예측값과 실제 $y_i$값의 loss를 계산하여 합한, model들의 Loss를 구하는 term이고, $\sum_k \Omega (f_k)$이 부분이 model의 일반화 term이다.
Objective function을 보면, parameter로 함수 $\phi$를 사용한다. 때문에 line search와 같은 방법으로 모든 함수들을 다 확인해야 하는 비효율적인 방법을 써야 한다. (즉 Euclidean space를 사용한 optimization이 불가능하다)
Gradient Tree Boosting (Article 2.2)
Boosting 방법이 점차 base learner를 더하는 방법으로 진행되는 것을 이용하여 (additive training) 위 식을 optimization이 가능하게끔 바꿔보자.
$$\hat{y}_i^t = \sum_{k=1}^t f_k(x_i) = \hat{y}_i^{t-1} + f_t(x_i)$$
$t$번째 prediction은 $t-1$번째 prediction에 $t$번째 base learner $f_t(x_i)$를 add하여 구한다. 위의 Objective function에 위 식을 대입해보자. (또한 $\sum_k \Omega (f_k)$를 $\Omega (f_t)$로 축약하였다.)
$$\mathcal{L}^{(t)} = \sum_i l(y_i,\hat{y}_i^{t-1} + f_t(x_i)) + \Omega (f_t)$$
이 식을 전개하는 과정에서 Taylor Expansion이 사용된다. 어떤 것인지 한번 알아보자.
- Taylor Expansion (Taylor Series)
Taylor Expansion은 미지의 함수 $f(x) = p_\infty (x)$를 다항함수로 근사하여 표현하는 방법이다.
$$\begin{align*}p_n(x) &= f(a) + f^\prime (a) (x-a) + \frac{f^{\prime\prime} (a)}{2!} (x-a)^2 + \cdots + \frac{f^{(n)} (a)}{n!} (x-a)^n\\&=\sum_{k=0}^n \frac{f^{(k)} (a)}{k!} (x-a)^k\end{align*}$$
$x$가 $a$ 근방일 때 위 근사식이 성립한다.
어떻게 위와 같은 근사가 성립할까?
예를 들어보자. 어떠한 $k$회 미분가능한 함수 $f$와 $p$가 있다고 할 때,
$$f^{\prime} (a) = p^{\prime} (a)$$
$$f^{\prime\prime} (a) = p^{\prime\prime} (a)$$
$$\vdots$$
$$f^{(\alpha)} (a) = p^{(\alpha)} (a) \;\;\;\; (\alpha < k)$$
이라면, 두 함수는 도함수에 대하여 같음을 보일수록 $a$의 근방에서 더 유사하다고 할 수 있을 것이다.
이러한 생각에 기반하여 근사식을 위의 Taylor Expansion의 형태로 구성하였다. 위 식을 살펴보면 원본 함수와 근사식의 도함수가 모두 일치함을 쉽게 보일 수 있다.
위의 Taylor Expansion을 다르게 쓰는 경우도 있다.
$$\begin{align*}f(x+\Delta x) &= f(x) + f^\prime (x) \Delta x + \frac{f^{\prime\prime} (x)}{2!} \Delta x^2 + \cdots + \frac{f^{(n)} (x)}{n!} \Delta x^n\\&=\sum_{k=0}^n \frac{f^{(k)} (x)}{k!} \Delta x^k\end{align*}$$
표기법이 좀 달라졌지만 의미는 동일하다.
우리는 여기 두번째 표기법을 따라서 Objective function을 전개해볼 것이다. 또한 Approzimation하여 이계 도함수까지만 Taylor Expansion을 전개하자.
$$f(x+\Delta x) \simeq f(x) + f^\prime (x) \Delta x + \frac{1}{2} f^{\prime\prime} (x)\Delta x^2$$
$l(y_i,\hat{y}_i^{t-1} + f_t(x_i))$에 적용해보자.
$$l(y_i,\hat{y}_i^{t-1} + f_t(x_i)) \simeq l(y_i,\hat{y}_i^{t-1}) + \partial_{\hat{y}^{t-1}}l(y_i,\hat{y}_i^{t-1}) f_t(x_i) + \frac{1}{2} \partial_{\hat{y}^{t-1}}^2l(y_i,\hat{y}_i^{t-1}) f_t(x_i)^2$$
표기가 너무 길어지니, $g_i = \partial_{\hat{y}^{t-1}}l(y_i,\hat{y}_i^{t-1})$ 그리고 $h_i=\partial_{\hat{y}^{t-1}}^2l(y_i,\hat{y}_i^{t-1})$로 치환하여 표기하자.
$$l(y_i,\hat{y}_i^{t-1} + f_t(x_i)) \simeq l(y_i,\hat{y}_i^{t-1}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2$$
Objective function은 아래와 같이 바뀌게 된다.
$$\mathcal{L}^{(t)} = \sum_i \big[l(y_i,\hat{y}_i^{t-1}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2\big] + \Omega (f_t)$$
여기서 $l(y_i,\hat{y}_i^{t-1})$ 은 상수이다. 따라서 Objective function을 최소화 하는 것에 영향을 주지 않는다. 이 항을 제거한 Objective function을 $\tilde{\mathcal{L}}^{(t)}$이라 한다.
$$\tilde{\mathcal{L}}^{(t)} = \sum_i \big[g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2\big] + \Omega (f_t)$$
위에서 $\Omega(f) = \gamma T + \frac{1}{2} \lambda ||w||^2$라고 정의하였다. 다시 원래 식을 대입하자.
$$\tilde{\mathcal{L}}^{(t)} = \sum_i \big[g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2\big] + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2\;\;\;\;\;\;(||w||^2=\sum_{j=1}^T w_j^2)$$
이제 Tree의 관점에서 Loss를 보기 위해서 $T$로 $\sum$식을 병합할 것이다. 위 식에서 각 항에 대하여 아래와 같이 변경할 수 있다.
$$\sum_{i=1}^n g_i f_t(x_i) = \sum_{j=1}^T \big(\sum_{i\in I_j} g_i\big) w_j$$
좌측항을 보면, $n$개의 instance 각각에 대한 1차 미분값 $g_i$와 tree의 결과값 $f_t(x_i)$를 곱해서 더해준다.
우측항을 보면, $T$개의 tree leaf node에 대한 leaf $j$의 instance 들의 1차 미분값 $g_i$와 leaf node에 지정된 weight $w_j$를 곱해서 더해준다.
모든 instance각각에 대하여 결과를 계산한 합과, leaf node에 포함되는 instance들을 모아서 계산하고 합한 것은 같다.
동일한 변환을 다음 항에도 적용하자.
$$\sum_{i=1}^n \frac{1}{2} h_i f_t(x_i)^2 = \frac{1}{2}\sum_{j=1}^T \big(\sum_{i\in I_j} h_i\big) w_j^2$$
$n$개의 instance 각각에 대한 2차 미분값 $h_i$와 tree의 결과값 $f_t(x_i)^2$를 곱해서 더해준것과 $T$개의 tree leaf node에 대한 leaf $j$의 instance 들의 2차 미분값 $h_i$와 leaf node에 지정된 weight $w_j^2$를 곱해서 더해준것은 같다.
위 변환을 적용하여 Objective function을 정리하면 아래와 같다.
$$\tilde{\mathcal{L}}^{(t)} = \sum_{j=1}^T\bigg[ \big(\sum_{i\in I_j} g_i\big) w_j +\frac{1}{2}\big(\sum_{i\in I_j} h_i + \lambda \big) w_j^2 \bigg] + \gamma T$$
위 Objective function이 최소값인 최적값의 조건은 미분값이 0이어야 한다. 미분을 쉽게 하기 위해서 각 항을 치환해서 미분해보자.
$$G_j = \sum_{i\in I_j} g_i$$
$$H_j = \sum_{i\in I_j} h_i$$
$$x = w_j$$
$$\tilde{\mathcal{L}}^{(t)} = \sum_{j=1}^T\bigg[ \big(G_j\big)x +\frac{1}{2}\big(H_j + \lambda \big) x^2 \bigg] + \gamma T$$
$x$로 미분하면,
$$G_j + (H_j + \lambda) x = 0 \;\;\;\;\rightarrow \;\;\;\;x^* = -\frac{G_j}{H_j+\lambda}$$
$$w_j^* = -\frac{\sum_{i\in I_j} g_i}{\sum_{i\in I_j} h_i + \lambda}$$
최소값을 알기 위해서 $x^*$를 다시 Objective function에 대입하자.
$$\begin{align*}\tilde{\mathcal{L}}^{(t)} &= \sum_{j=1}^T\bigg[ \big(G_j\big)\big(-\frac{G_j}{H_j+\lambda}\big) +\frac{1}{2}\big(H_j + \lambda \big) \big(-\frac{G_j}{H_j+\lambda}\big)^2 \bigg] + \gamma T\\&=-\frac{1}{2}\sum_{j=1}^T\bigg[\frac{G_j^2}{H_j+\lambda}\bigg] + \gamma T \\&=-\frac{1}{2}\sum_{j=1}^T\bigg[\frac{\big(\sum_{i\in I_j} g_i\big)^2}{\sum_{i\in I_j} h_i+\lambda}\bigg] + \gamma T\end{align*}$$
$$Structure\;score\;of\;tree\;:\;\tilde{\mathcal{L}}^{(t)}(q) =-\frac{1}{2}\sum_{j=1}^T\bigg[\frac{\big(\sum_{i\in I_j} g_i\big)^2}{\sum_{i\in I_j} h_i+\lambda}\bigg] + \gamma T$$
$$Optimal\;leaf\;weight\;:\;w_j^* = -\frac{\sum_{i\in I_j} g_i}{\sum_{i\in I_j} h_i + \lambda}$$
위 식을 optimal한 weight $w_j^*$를 가지는 트리의 구조 $q$에 대하여 score를 측정하는 measure function으로 사용할 수 있다. ($\frac{\big(\sum_{i\in I_j} g_i\big)^2}{\sum_{i\in I_j} h_i+\lambda}$이 커질수록 Loss가 감소한다)
여기서 잠깐 $\gamma T$와 $\lambda$에 대하여 짚고 넘어가자.
- $T$ : Number of terminal(leaf) nodes
- $\gamma$ : Penalty hyperparameter (for Pruning)
- $\lambda$ : Regularization hyperparameter
XGBoost는 base learner인 트리를 다 구성한 이후에 Generalization과 구조의 복잡도 감소를 위하여 밑에서(leaf)부터 Pruning(가지치기)를 진행한다. $\gamma$는 밑에서 더 자세히 다루겠지만, pruning 여부를 결정하는데 사용된다.
$\lambda$는 각 leaf node의 예측값(output value $w_j^*$)를 계산하는데 사용된다. 해당 결과는 이전 예측값 $h_i$와 $g_i$에 의해서 결정되는데, $\lambda$는 분모에 더해져 이전 예측값에 대한 sensitivity를 감소시킨다.
Gradient Tree Boosting (Article 2.2) (Cont.)
위에서 각 구조에 대한 Structure score function과 Optimal leaf weight를 구했다. 하지만 일반적으로 모든 가능한 Tree structure를 모두 시도해볼 수 없다. 때문에 Tree split 기준을 정하고, Greedy하게 분할하면서 최적의 tree를 만들어야 한다.
Tree split 기준으로 아래와 같은 Gain을 사용한다.
$$I = I_L \cup I_R$$
$$\mathcal{L}_{split} = \frac{1}{2}\bigg[\frac{\big(\sum_{i\in I_L} g_i\big)^2}{\sum_{i\in I_L} h_i+\lambda}+\frac{\big(\sum_{i\in I_R} g_i\big)^2}{\sum_{i\in I_R} h_i+\lambda}-\frac{\big(\sum_{i\in I} g_i\big)^2}{\sum_{i\in I} h_i+\lambda}\bigg] - \gamma$$
$$\;\;\;\;\;\;\;(1)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(2)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3)$$
$(1)$term은 Left node로 split된 instance들의 Gain이다. $(2)$term은 Right node로 split된 instance들의 Gain, 그리고 $(3)$term은 split 되기 전 원래 node의 instance들의 Gain이다.
우리의 목적은 분할이 완료 되었을 때 모든 Leaf node에 대한 Gain $\frac{\big(\sum_{i\in I_j} g_i\big)^2}{\sum_{i\in I_j} h_i+\lambda}$이 최대가 되도록 하는 것이다. 따라서 $\mathcal{L}_{split}$이 최대가 되는 split point를 찾는다. (분할한 이후 $I_L$과 $I_R$의 Gain이 클수록 $\mathcal{L}_{split}$이 크다)
위에서 $\gamma$가 pruning 여부를 결정하는데 사용된다고 언급했었다.
XGBoost는 base learner인 트리를 다 구성한 이후에 Generalization과 구조의 복잡도 감소를 위하여 밑에서 부터 Pruning(가지치기)를 진행한다.
완성된 Tree에 대하여 아래의 split point부터 Gain을 계산하고 $\gamma$를 뺀 Gain값이 음수라면 해당 split을 취소한다(Pruning). 하지만 Gain값이 음수여도 pruning하지 않는 경우가 있는데, 자신의 child node가 pruning되지 않고 남아있는 경우(Gain>0) 자신의 Gain이 음수이더라도 pruning하지 않는다.
잠시 Cover에 대하여 알아보자.
$\sum h_i$는 Hessian function들의 합으로, Cover라는 이름으로 불린다. 아래에서 다시 보겠지만, 이는 각 feature들이 전체 XGBoost 모델에 있어 data split과정에서 몇번 사용되었는지 나타낸다.
Structure score function과 Optimal leaf weight를 다시 가져와서 Regression을 하는 경우와 Classification을 하는 경우 어떻게 다른지 한번 비교해보자.
$$Structure\;score\;of\;tree\;:\;\tilde{\mathcal{L}}^{(t)}(q) =-\frac{1}{2}\sum_{j=1}^T\bigg[\frac{\big(\sum_{i\in I_j} g_i\big)^2}{\sum_{i\in I_j} h_i+\lambda}\bigg] + \gamma T$$
$$Optimal\;leaf\;weight\;:\;w_j^* = -\frac{\sum_{i\in I_j} g_i}{\sum_{i\in I_j} h_i + \lambda}$$
- Regression
Regression의 경우 일반적으로 아래와 같은 squared loss function을 사용한다.
$$l(y_i,\hat{y}^{(t-1)}) = \frac{1}{2} (y_i - \hat{y}^{(t-1)})^2$$
이때 $g_i$와 $h_i$를 계산해보자.
$$g_i = \partial_{\hat{y}^{t-1}}l(y_i,\hat{y}_i^{t-1}) = -(y_i - \hat{y}^{(t-1)})$$
$g_i$는 각 instance들의 residual에 -부호를 취한 값이 되고,
$$h_i=\partial_{\hat{y}^{t-1}}^2l(y_i,\hat{y}_i^{t-1}) = 1$$
$h_i$는 상수 1이 된다.
각 결과를 Structure score function과 Optimal leaf weight에 대입하면, (어떤 의미인지 보기 위해서 $\frac{1}{2}$와 $\gamma T$는 생략했다)
$$Structure\;score\;of\;tree\;:\;\tilde{\mathcal{L}}^{(t)}(q) =\frac{Sum\;of\;residuals^2}{Number\;of\;residuals+\lambda}$$
$$Optimal\;leaf\;weight\;:\;w_j^* = \frac{Sum\;of\;residuals^2}{Number\;of\;residuals +\lambda}$$
이 경우 Cover는 $Number\;of\;residuals$로, 상수이다. 때문에 Regression의 경우 이전 예측 결과가 Cover에 영향을 주지 않는다.
- Classification
Classification의 경우 일반적으로 아래와 같은 Log loss function을 사용한다.
$$l(y_i,\hat{y}^{(t-1)}) = -[y_i \log(\hat{y}^{(t-1)}) + (1-y_i)\log(1-\hat{y}^{(t-1)})]$$
Classification에서 예측값 $\hat{y}^{(t-1)}$은 0~1사이 확률값임으로 $p_i$라고 적도록 하자.
$$l(y_i,\hat{y}^{(t-1)}) = -[y_i \log(p_i) + (1-y_i)\log(1-p_i)]$$
이제 $g_i$와 $h_i$를 계산해보자.
$$g_i = \partial_{\hat{y}^{t-1}}l(y_i,\hat{y}_i^{t-1}) = -(y_i - \hat{y}^{(t-1)}) = -(y_i-p_i)$$
$g_i$는 각 instance들의 residual에 -부호를 취한 값이 되고,
$$h_i=\partial_{\hat{y}^{t-1}}^2l(y_i,\hat{y}_i^{t-1}) = \hat{y}^{(t-1)}(1-\hat{y}^{(t-1)}) = p_i(1-p_i)$$
$h_i$는 이전 예측값에 대하여 $p_i(1-p_i)$이 된다.
각 결과를 Structure score function과 Optimal leaf weight에 대입하면, ($p_i = Previous\;probability_i$)
$$Structure\;score\;of\;tree\;:\;\tilde{\mathcal{L}}^{(t)}(q) =\frac{Sum\;of\;residuals^2}{\sum p_i(1-p_i)+\lambda}$$
$$Optimal\;leaf\;weight\;:\;w_j^* = \frac{Sum\;of\;residuals^2}{\sum p_i(1-p_i) +\lambda}$$
이 경우 Cover는 $\sum p_i(1-p_i)$로, Classification의 경우 이전 예측 결과가 Cover에 영향을 준다.
Shrinkage and Column Subsampling (Article 2.3)
- Shirinkage
Shirinkage는 새롭게 추가되는 Tree에 대하여 $\eta$를 곱하여 각 Tree의 영향력을 조절한다.(줄여준다). 앞서 GBM에서 알아보았음으로 자세한 내용은 생략한다.
- Column Sampling
일반적으로 Data를 Row major로 사용하는데 반해, XGBoost에서는 Column major로 사용한다. 이때 Column Subsampling을 통해 sampling된 variable만을 사용해 학습을 시도한다. 이를 통해 Overfitting을 방지하고, 학습 시간을 단축할 수 있다. 더 자세한 내용은 뒤에서 알아보자.
지금까지 XGBoost의 알고리즘을 이해하기 위해 필요한 수식적인 도출과정과 사전지식을 모두 알아보았다. 이제 본격적으로 Split Finding Algorithms이 어떤게 있고 어떻게 진행되는지 알아보자.
Basic Exact Greedy Algorithm (Article 3.1)
가장 먼저 알아볼 것은 Greedy하게 모든 경우의 수를 다 탐색하는 방법이다. Pseudo-code는 아래와 같다.
Input : $I$, instance set of current node
Input : $d$, feature dimension
$gain \leftarrow$ 0
$G \leftarrow \sum_{i\in I} g_i$
$H \leftarrow \sum_{i\in I} h_i$
for $k = 1$ to $m$ do :
$G_L\leftarrow 0$
$H_L\leftarrow 0$
for $j$ in $sorted(I,by\;x_{jk})$ do :
$G_L\leftarrow G_L + g_j$
$H_L\leftarrow H_L + h_j$
$G_R\leftarrow G - G_L$
$H_R\leftarrow H - H_L$
$score \leftarrow \max \big(score,\;\frac{G_L^2}{H_L +\lambda} +\frac{G_R^2}{H_R +\lambda}-\frac{G^2}{H +\lambda}\big)$
end
end
Output : Split with max $score$
매번 Sorting하는 것은 비효율적임으로, 처음 모든 data를 sorting 해놓고 알고리즘을 시작한다. 모든 가능한 point에 대하여 $\mathcal{L}_{split}$를 최대화 하는 split point를 찾는다.
이 방법은 모든 경우의 수를 확인함으로 최적해를 찾는 것이 보장된다는 장점이 있다. 하지만 매우 느리고 data가 너무 많기 때문에 모든 data가 memory에 한번에 할당될 수 없고, 병렬처리 또한 불가능하다는 단점이 있다.
(여기서 부터가 XGBoost의 핵심이다 !)
Approximation Algorithm (Article 3.2)
위와 같은 단점을 보완하는 방법이 Approximation algorithm이다. 최적해의 근사를 통해 병렬처리가 가능해지고 매우 빠른 수행 속도를 보인다.
알고리즘을 보기 앞서 Percentile에 따라 candidate splitting points를 구성한다는 것이 어떤 것인지 알아보자.
- Percentile (백분위수)
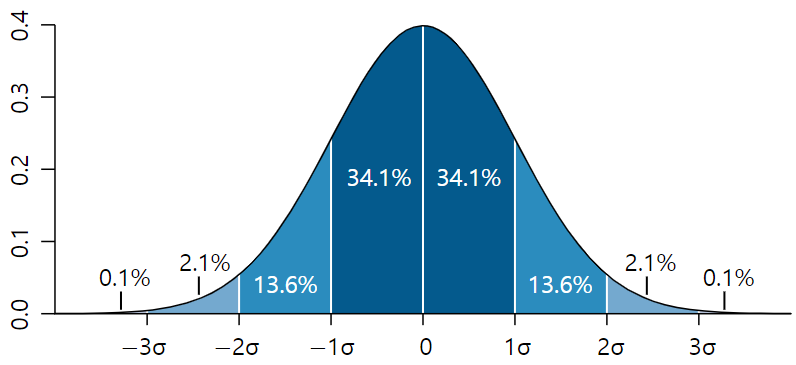
percentile이란 크기가 있는 값들을 순서대로 나열했을 때 백분율로 나타낸 특정 위치 값을 나타내는 용어이다. 만약 데이터가 정규분포를 따른다면 아래와 같이 분포할 것이다.
(물론 실제 data는 더 다양한 분포로 나타날 것이다. 사실 위와 같은 분포도를 생각하는 것 보다 아래의 예시를 보는 것이 더 이해하기 쉽다)
- Candidate splitting point
우선 한 variable에 대하여 아래와 같은 분포를 가진다고 생각해보자.
그리고 candidate split point를 기준으로 10개의 bucket을 구성한다. (위 그림에서 빨간 선으로 나눠진 구간들이 각 bucket이다.
이제 각 bucket에 대하여 Gradient를 계산하여 최적의 split point 10개를 뽑는다. 그 중에서 가장 $score$이 높은 split point를 선택한다. (여기서 주의할 점은 한 bucket의 split point를 선택할 때 그 bucket의 원소들에 대해서만 gradient를 계산한다는 점이다. 모든 원소들의 gradient를 계산하는게 아니다!)
for $k = 1$ to $m$ do :
Propose candidate S_k = \{s_{k1},s_{k2},\cdots,s_{kl}\} by percentiles on feature $k$.
Proposal can be done per tree (global), or per split (local)
end
for $k=1$ to $m$ do :
$G_{kv} \leftarrow \sum_{j\in \{j|s_{k,v}\, \geq x_{jk} > s_{k,v-1}\;\}} g_j$
$H_{kv} \leftarrow \sum_{j\in \{j|s_{k,v}\, \geq x_{jk} > s_{k,v-1}\;\}} h_j$end
Follow same step as in previous section to find max score only among proposal splits.
위 항목이 위의 Exact Greedy Algorithm의 pseudo-code의 gradient를 계산하는 부분을 대체한다고 생각하면 된다.
자세히 살펴보면,
$G_{kv} \leftarrow \sum_{j\in \{j|s_{k,v}\, \geq x_{jk} > s_{k,v-1}\;\}} g_j$
$H_{kv} \leftarrow \sum_{j\in \{j|s_{k,v}\, \geq x_{jk} > s_{k,v-1}\;\}} h_j$
위 수식에서 Gradient를 계산하는 과정이 $s_{k,v}\, \geq x_{jk} > s_{k,v-1}$, 한 Bucket에 원소들에 대해서만 수행되는 것을 확인할 수 있다.
그렇다면 Bucket을 몇개 만들지, 어떻게 결정할까?
$\epsilon$은 Percentile을 몇개로 나눌지 결정하는 Approximation factor 이다. Candidate split point의 개수는 $\frac{1}{\epsilon}$이다. (Bucket의 개수 또한 같을 것이다)
예를들어 $\epsilon = 0.01$ 이라면 Candidate split point의 개수는 $\frac{1}{0.01} = 100$개일 것이다.
$\epsilon$에 따른 Candidate split point 선택방법은 두가지가 있다.
- Global variant
알고리즘이 시작할 때 $\epsilon$에 따라 모든 Candidate를 구성하고 이후 split 과정에서도 이 Candidate를 계속 사용한다.
처음에 선택된 Candidate가 이후 적은 instance를 가지는 node에 대해서도 유지되기 때문에 초기 $\epsilon$ 설정을 작게하여 Candidate가 많게 해야한다.
- Local variant
알고리즘의 진행과정 중 Split이 된 이후마다 $\epsilon$에 따라 현재 node에 대하여 Candidate를 재구성한다. Global variant보다 훨씬 많은 Candidate를 재탐색 하고, 더 많은 경우를 탐색한다. 때문에 크고 깊은 Tree에 대하여 더 좋은 성능을 보인다.
Weighted Quantile Sketch (Article 3.3)
위에서 Approximation factor $\epsilon$을 사용하여 $\frac{1}{\epsilon}$ 만큼의 Candidate split point를 선택한다고 하였다. 이것이 정확히 어떤 의미인지, 왜 이렇게 하는지 알아보자.
일반적으로 Candidate를 선택하기 위해서 percentile을 사용한다고 하였다. 이를 위해서는 모든 데이터에 대한 분포 히스토그램을 구성해야 한다.
Multi-set $\mathcal{D}_k = \{(x_{1k},h_1),(x_{2k},h_2),\cdots,(x_{2k},h_2)\}$ 이 있다고 가정하자. 우리는 이 Multi-set에 대하여 Rank function $r_k\;:\;\mathbb{R}\rightarrow[0,+\infty)$를 아래와 같이 정의한다.
$$r_k(z) = \bigg( \frac{1}{\sum_{(x,h)\in \mathcal{D}_k} h} \bigg) \bigg( \sum_{(x,h)\in \mathcal{D}_k,x<z} h \bigg)$$
위 함수는 $z$번째 보다 작은 $x$들의 $h$ 누적값을 계산하고 그 비율을 구한다.
이를 통해 아래와 같은 조건을 만족하는 Candidate split points $\{s_{k1},s_{k2},\cdots,s_{kl}\}$ 를 찾는다.
$$|r_k(s_{k,j}) - r_k(s_{k,j+1})| < \epsilon,\;\;\;s_{k1} = \min_i x_{ik},\;s_{kl} = \max_i x_{ik}$$
어떻게 동작하는지 한번 예시를 들어보자.
100개의 data points $\{x_1,x_2,\cdots,x_{100}\}$ ($h$는 생략)가 있다고 할 때, 이들 모두는 split point가 될 가능성이 있다. 이 중에서 Candidate를 뽑는것이 목적이다.
우선 $s_{k1} = \min_i x_{ik},\;s_{kl} = \max_i x_{ik}$로 지정하고 $r_k(z)$를 계속 누적해 나가면서,
$|r_k(s_{k,1}) - r_k(s_{k,2})| < \epsilon$를 만족하는 $x_i$를 찾는다. 찾았다면 $s_{k,2} = x_i$이다. 예시를 위해 $s_{k,2} = x_9$라고 하자.
그렇다면 $x_1$부터 $x_9$까지의 구간은 $\epsilon$만큼의 비율로 구성된다. (정확히는 미만)
위 과정을 계속 진행하여 Candidate로 $\{ x_1,x_9,\cdots, x_{89},x_{100}\}$을 선택완료했다면, 각 구간의 비율은 $\epsilon$정도일 것이고, 구간의 수는 (대략) $\frac{1}{\epsilon}$개 일 것이다.
그런데 왜 $h_i$를 비율의 기준 weight로 사용한 것일까?
정확히 말해서, 위의 설명과 수식은 좀 괴리가 있다. 왜냐하면 설명을 쉽게 하기 위해서 설명은 Quantile sketch방법을 말하지만, 수식은 Weighted quantile sketch를 나타내기 때문이다.
그냥 Quantile sketch방법은 위에서 설명한 것 처럼 분포 히스토그램을 구성하여 각 Quantile의 데이터 개수가 같게 나누어준다.(그냥 누적 데이터 비율이 분할 기준)
반면, Weighted quantile sketch방법은 위의 수식이 $h_i$를 사용하듯이 각 Quantile의 sum of weight가 같게 나누어준다.
위에서 Cover에 대하여 알아보았듯이 Regression model이라면, weight가 모두 1일 것이다. 하지만 Classification model이라면,
weight $h_i = (Previous\;Probability_i) \times (1-Previous\;Probability_i)$이다.
$Previous\;Probability_i$는 이전 base learner tree에서 예측한 결과 값이다.
$h_i$를 weight로 사용함으로써 Cover에 대한 percentile을 구성하게 되고, 이를 통해 Leaf node의 instance들이 균등하게 분포하도록 Candidate split point를 선택한다.
위에서 Object function을 다시 가져와보자. 이 식을 변형하여 $h_i$가 weight임을 보일것이다.
$$\begin{align*}\tilde{\mathcal{L}}^{(t)} &= \sum_i \big[g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2\big] + \Omega (f_t)\\&=\sum_i \big[g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2 + \frac{g_i^2}{2h_i}\big]-\sum_{i=1}^n \frac{g_i^2}{2h_i} + \Omega (f_t)\end{align*}$$
여기서 추가된 $-\sum_{i=1}^n \frac{g_i^2}{2h_i}$항은 이전 값들로 계산되는 상수항 임으로 $constant$라고 나타내자.
$$\begin{align*}\cdots &=\sum_i \big[g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2 + \frac{g_i^2}{2h_i}\big]+ \Omega (f_t) + constant\\&=\sum_i \frac{1}{2} h_i\big[ f_t(x_i)^2 +2\frac{g_i f_t(x_i)}{h_i} + (\frac{g_i}{h_i})^2\big]+ \Omega (f_t) + constant \\&=\sum_i \frac{1}{2} h_i \big(f_t(x_i) -(-\frac{g_i}{h_i})\big)^2+ \Omega (f_t) + constant\end{align*}$$
(여기서 논문의 식과 $-\frac{g_i}{h_i}$부분의 $+,-$가 다르다... 다른 자료를 찾아봐도 sign reverse를 해야 한다고만 나와있고 이유가 적혀있지는 않았다. 논문의 표기 오류인가 싶기도 한데 그럴 가능성은 적고, 아마 내가 모르는 다른 이론적 이유가 있는 것 같다. 지금 당장 이해하는데 큰 문제는 없음으로, 이후 공부해 보고 알게 된다면 추가하도록 하겠다!)
결론적으로 도출된 식을 살펴보면, label $-\frac{g_i}{h_i}$에 대한 weighted squared loss임을 확인할 수 있다. 여기서 $h_i$가 weight로 사용된다.
Sparsity-aware Split Finding (Article 3.4)
일반적으로 이론적으로 모델을 구성하고 수식으로 표현할 때 Data는 누락된 value가 없는 Dense Data이다. 하지만 현실 문제를 다룰 때는 누락되거나 축약되어 소실된 Sparse Data가 많다.
논문에서 제시하는 Sparsity의 주요한 원인은 아래와 같다.
- Presence of missing values in the data.
- Frequent zero values
- Artifacts of feature engineering such as one-hot encoding
XGBoost에서는 sparsity aware이라는 방법론을 제시한다. Default한 decision을 학습하여 sparsity한 data가 주어지더라도 데이터를 못 쓰는 것이 아니라 유의미한 동작이 가능하게 한다.
Psudo-code는 아래와 같다.
Input : $I$, instance set of current node
Input : $I_k = \{i\in I | x_{ik} \neq missing\}$, non-missing dataInput : $d$, feature dimension
Also applies to the approximate setting, only collect statistics of non-missing entries into buckets.
$gain \leftarrow$ 0
$G \leftarrow \sum_{i\in I} g_i$
$H \leftarrow \sum_{i\in I} h_i$
for $k = 1$ to $m$ do :
// Enumerate missing value goto right.
$G_L\leftarrow 0$
$H_L\leftarrow 0$
for $j$ in $sorted(I,\;ascent\;order\;by\;x_{jk})$ do :
$G_L\leftarrow G_L + g_j$
$H_L\leftarrow H_L + h_j$
$G_R\leftarrow G - G_L$
$H_R\leftarrow H - H_L$
$score \leftarrow \max \big(score,\;\frac{G_L^2}{H_L +\lambda} +\frac{G_R^2}{H_R +\lambda}-\frac{G^2}{H +\lambda}\big)$
end
// Enumerate missing value goto left.
$G_L\leftarrow 0$
$H_L\leftarrow 0$
for $j$ in $sorted(I,\;ascent\;order\;by\;x_{jk})$ do :
$G_L\leftarrow G_L + g_j$
$H_L\leftarrow H_L + h_j$
$G_R\leftarrow G - G_L$
$H_R\leftarrow H - H_L$
$score \leftarrow \max \big(score,\;\frac{G_L^2}{H_L +\lambda} +\frac{G_R^2}{H_R +\lambda}-\frac{G^2}{H +\lambda}\big)$
end
end
Output : Split and default directions with gain
아이디어는 단순하다. missing value인 data들을 모두 한쪽을 몰아놓고, 둘 중 더 좋은 score를 내는 방향으로 분류하는 것이다.
각 과정을 보면 우선 missing value인 data들을 오른쪽으로 몰아넣고, Score를 계산한다.
그리고 missing value인 data들을 왼쪽으로 몰아넣고, Score를 계산한다. 그리고 이 둘 중 더 Score가 높은 쪽으로 missing value인 data들을 split한다.
논문에서는 이러한 방법을 통해 Sparse Data에 대해서도 좋은 성능을 보임을 제시하고 있다.
지금까지 XGBoost의 방법론과 알고리즘에 대하여 알아보았다. 4. System Design 부터는 XGBoost가 하드웨어적으로 어떻게 최적화 방법을 사용하였는지 아래의 내용들을 제시하고 있다. 간단하게 요약정리만 해보았다.
- Column Block for Parallel Learning (4.1)
Column major로 저장하여 블록단위로 Parallel learning이 가능하게 하였다.
- Cache-aware Access (4.2)
IO speed가 Cache > Memory > Disc 순으로 빠르다는 점을 고려하여, 자주 사용하는 statistic $g_i$, $h_i$, $score$ 등을 항상 cache에 저장하도록 한다. 이를 통해 속도를 향상한다.
- Blocks for Out-of-core Computation (4.3)
대용량의 data가 disk에서 memory로 load되는 시간을 단축하기 위해서 Block Compression, Block Sharding과 같은 방법을 사용한다.
논문에서 하는 설명들이 어려운 내용이 아니라서(물론 깊게 들어가면 어렵지만) 해당 부분은 논문을 읽어보는 것을 추천한다!
※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의, StatQuest - XGBoost영상, 논문을 통해 공부한 내용을 정리하여 작성되었습니다.





댓글
댓글 쓰기