Graph-based SSL

-
05_3 : Semi-Supervised Learning : Graph-based SSL


이번 글에서는 Graph 기반의 Semi-Supervised Learning을 알아보자.

Graph-based SSL

가장 기본적인 아이디어는 우리에게 주어진 Data instance들을 Graph의 Node로 표현하고, 각 Data들의 유사성을 Edge로 표현하는 것이다. 여기서 가정은 아래와 같다.
  • A graph is given on the labeled and unlabeled data
  • Instances connected by heavy edge tend to have the same label
구성된 Graph에 대하여 두 instance가 heavy edge, 강한 연결관계를 갖고있다면 두 Instance가 동일한 label일 가능성이 높다고 간주한다.



Graph Construction

  • Nodes : $X_l \cup X_u$
  • Edges : Similarity weights computed from features, e.g.
    • K-nearest neighbor graph : Unweighted (0 or 1 weights)
    • Fully connected graph, weight decays with distance
$$ w_{ij} = exp \big(\frac{-||x_i - x_j ||^2} { \sigma^2 } \big) $$
    • $\epsilon$-radius graph
K-nearest neighbor (KNN) 방법은 가장 가까운 K개를 1 weight로 연결한다. 때문에 data의 밀도를 고려하지 못하는 단점이 있다.

Fully connected graph의 경우, 모든 경우를 표현하지만, Graph의 크기가 너무 커진다는 단점이 있다.

$\epsilon$-radius graph 방법은, 거리가 일정 Cut-off 이하인 Node들 만을 Edge로 연결한다. 이 경우 data의 밀도를 고려 가능하지만, 모든 instance가 연결된다는 보장이 없다는 단점이 있다. (isolation point나, 그룹간 단절이 일어날 수 있다) 때문에 일반적으로 Minimum Spanning Tree(MST)와 같은 알고리즘을 사용해 독립된 그룹들을 적어도 하나씩의 Edge로 이어주는 작업을 수행해 준다. 이렇게 해 주어야 Label이 모두 Propagate가능하다.



위와 같은 Graph construction이 완료되면 이제 heavy edge 관계를 찾아, Unlabeled data를 labeling해준다.
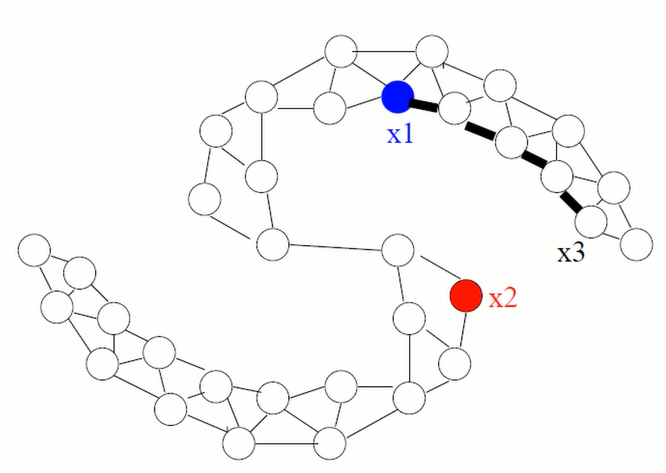
위 예시를 보자. Labeled data $x_1, x_2$가 있고, Unlabeled data $x_3$가 있다. 굵은 선 Edge들이 heavy edge라고 할 때 $x_3$의 label은 파란색일 가능성이 더 높다.
$$P(blue) > P(red)$$



Optimization problem

이제 우리가 원하는 동작을 수행 가능하도록 최적화 문제를 formulate 해보자.
  • The mincut algorithm
▶Fix $y_l$ and find $y_u \in \{0,1\}^{n-l}$ to minimize $\sum_{i,j} w_{ij} | y_i-y_j |$

Labeled 된 data의 값은 절대 변하면 안된다. 이 값을 고정하고, $\sum_{i,j} w_{ij} | y_i-y_j |$ 식을 최소화 하는 $y_u$값들을 찾는다.  이때 $y_u$값들은 반드시 0 혹은 1이어야 한다.

두 instance간의 거리가 가까워서 weight $w_{ij}$가 크다면, 두 instance의 label이 같아야 한다. 반면 $w_{ij}$가 작다면, 두 instance label이 같지 않아도 된다.


▶Equivalently, solve the optimization problem :
$$\min_{y\in \{0,1\}^n} \infty \sum_{i=1}^l (y_i - y_{li})^2 + \sum_{i,j} w_{ij} (y_i - y_j)^2$$

Labeled 된 data의 값을 고정하는 조건을 $\infty \sum_{i=1}^l (y_i - y_{li})^2$과 같이 나타낸다. 만약 하나라도 label과 값이 다르다면 $\infty$가 곱해져서 최소화 문제를 만족하지 못할 것이다. 그리고 나머지 $\sum_{i,j} w_{ij} (y_i - y_j)^2$ term은 위의 식에서 norm으로 차이를 나타내는 것을 미분을 쉽게하기 위해 제곱항으로 나타낸다.

이 최적화 문제는 Combinatorial problem으로, polynomial time solution이 존재한다.



  • Harmonic function
위의 제약조건을 좀 완화시켜보자. 먼저 $y_u$값이 반드시 Discrete한 0 또는 1 값을 가져야 한다는 제약조건을 Harmonic function $f$를 사용하여 Continuous 한 값을 가질 수 있다고 완화(Relaxation)할 수 있다.
$$f(x_i) = y_i\;\;\;\;for\;\;i=1,2,\cdots, l$$

그렇다면 Energy function를 minimize 하는 $f$를 찾는 것이 우리의 목표가 된다.
$$\sum_{i\sim j} w_{ij} (f(x_i) - f(x_j))^2 $$

이때의 Solution은 Gaussian random field의 평균이 되기 때문에, $f(x_i)$는 neighbor들의 평균이 된다.
$$f(x_i) = \frac{\sum_{j\sim i} w_{ij} f(x_j)}{\sum_{j\sim i} w_{ij}},\;\;\;\; \forall x_i \in X_u$$



위 식을 Graph Laplacian을 사용해 표현해보자.
  • Graph Laplacian
우선 graph Laplacian이 무엇인지 알아보자.
$X_l \cup X_u$ 총 $n$개의 instance들에 대하여 $n \times n$ weight matrix $W$가 있다고 가정하자. 이 행렬은 Symmetric 하고 non-negative하다.

이때 Diagonal degree matrix $D$와 Graph Laplacian matrix $\Delta$는 다음과 같이 정의된다.
$$D\;:\;D_{ii} = \sum_{j=1}^n W_{ij} $$
$$\Delta = D-W$$


아래 예시에서 Degree matrix $D$에 Adjacency matrix $W$를 빼서 Laplacian matrix $\Delta$를 만든 것을 확인할 수 있다.



이제 Graph Laplacian을 사용하면 위의 Energy function을 행렬을 사용해 나타낼 수 있다. 
$$\frac{1}{2}\sum_{i\sim j} w_{ij} (f(x_i) - f(x_j))^2 = \mathbf{f}^T \Delta \mathbf{f}$$

여기서 $\mathbf{f}$는 각 $x_i$값들에 대한 $f(x_i)$값을 차례로 모아놓은 vector이다.

어떻게 두 식이 같아지는지 증명해보자. 먼저 우측항을 정리해보자.
$$\begin{align*}\mathbf{f}^T \Delta \mathbf{f} &= \mathbf{f}^T (D-W) \mathbf{f}\\&=\mathbf{f}^T D \mathbf{f} - \mathbf{f}^T W \mathbf{f}\end{align*}$$
$$\begin{align*}\mathbf{f}^T D \mathbf{f} &= \begin{bmatrix}f(x_1)&\cdots &f(x_n)\end{bmatrix}\begin{bmatrix}D_{11} & \cdots & 0\\ & \ddots & \\ 0 & \cdots & D_{nn} \end{bmatrix} \begin{bmatrix}f(x_1)\\ \vdots \\ f(x_n)\end{bmatrix}\\ &=f(x_1)D_{11}f(x_1) + \cdots  + f(x_n)D_{nn}f(x_n) \\ &= \sum_{i=1}^n \sum_{j=1}^n f(x_i) w_{ij} f(x_i) \end{align*}$$


$$\begin{align*}\mathbf{f}^T W \mathbf{f} &= \begin{bmatrix}f(x_1)&\cdots &f(x_n)\end{bmatrix}\begin{bmatrix}W_{11} & \cdots & W_{1n}\\ & \ddots & \\ W_{n1} & \cdots & W_{nn} \end{bmatrix} \begin{bmatrix}f(x_1)\\ \vdots \\ f(x_n)\end{bmatrix}\\ &=f(x_1)\sum_{i=1}^n w_{1i}f(x_i) + \cdots  + f(x_n)\sum_{i=1}^n w_{ni}f(x_i)\\ &= \sum_{i=1}^n \sum_{j=1}^n f(x_i) w_{ij} f(x_j) \end{align*}$$


$$\begin{align*}\mathbf{f}^T \Delta \mathbf{f} &=\sum_{i=1}^n \sum_{j=1}^n f(x_i) w_{ij} f(x_i) - \sum_{i=1}^n \sum_{j=1}^n f(x_i) w_{ij} f(x_j) \\ &= \sum_{i=1}^n \sum_{j=1}^n w_{ij}(f(x_i)^2 - f(x_i)f(x_j) )\end{align*}$$


이제 좌측항을 정리하여 우측항과 같아짐을 보일 것이다.

$\sum_{i\sim j}$는 $i$와 $j$가 다른 모든 경우를 합산한다. 그런데 $(f(x_i) - f(x_j))$식을 보면 $i=j$인 경우 0이 됨을 확인할 수 있다. 따라서 $\sum_{i\sim j}$을 $\sum_{i=1}^n \sum_{j=1}^n$으로 표현 가능하다.
$$\begin{align*} \frac{1}{2}\sum_{i\sim j} & w_{ij} (f(x_i) - f(x_j))^2 \\ &= \sum_{i=1}^n \sum_{j=1}^n \frac{1}{2} w_{ij} (f(x_i) - f(x_j))^2 \\ &=\sum_{i=1}^n \sum_{j=1}^n \frac{1}{2} w_{ij} (f(x_i)^2 + f(x_j)^2 - 2f(x_i)f(x_j))\\ &=\sum_{i=1}^n \sum_{j=1}^n w_{ij} (f(x_i)^2  - f(x_i)f(x_j))\end{align*}$$

위의 유도과정을 통해 좌측항과 우측항이 서로 같음을 확인할 수 있다.



  • Harmonic solution with Laplacian
이제 위의 Laplacian matrix를 사용하여, 우리가 최소화 하고자 하는 Energy function은 아래와 같이 표현할 수 있다.
$$L = \min_{f} \infty \sum_{i=1}^l (f(x_i) - y_i)^2 + \mathbf{f}^T \Delta \mathbf{f}$$

우리는 Harmonic function을 사용하여 $y_u$값이 반드시 Discrete한 0 또는 1 값을 가져야 한다는 제약조건을 Continuous 한 값을 가질 수 있다고 완화(Relaxation)하였다($\mathbf{f}^T \Delta \mathbf{f}$). 

하지만 여전히 $y_l$값은 고정된다는 조건을 명심해야 한다($\infty \sum_{i=1}^l (f(x_i) - y_i)^2$).


이 경우의 최적해는 미분 값이 0이어야 한다.
$$\frac{\partial L}{\partial \mathbf{f}}= 0\;\;\;\;\Rightarrow \;\;\;\;\Delta \mathbf{f} = 0$$
※ Vector 미분 : $\frac{\partial (\mathbf{x})^T W (\mathbf{x})}{\partial \mathbf{x} } = 2W(\mathbf{x}) $


Laplacian matrix $\Delta$는 아래와 같이 분할하여 표현할 수 있다.
$$\Delta = \begin{bmatrix} \Delta_{ll} & \Delta_{lu} \\ \Delta_{ul} & \Delta_{uu} \end{bmatrix} $$

$\Delta f = 0$을 이용하여 Harmonic solution을 구해보자.
$$\Delta f = \begin{bmatrix} \Delta_{ll} & \Delta_{lu} \\ \Delta_{ul} & \Delta_{uu} \end{bmatrix} \begin{bmatrix} f_l \\ f_u \end{bmatrix} = 0$$
$$\Delta_{ul}f_l + \Delta_{uu}f_u = 0$$
$$f_u = -\Delta_{uu}^{-1} \Delta_{ul} y_l \;\;\;\;\;\;(y_l = f_l)$$



지금까지 설명에서는 그냥 Laplacian matrix을 사용했지만, 일반적으로 계산의 안정성을 위해 Normalized Laplacian matrix를 사용한다.
$$\mathcal{L} = D^{-\frac{1}{2}} \Delta D^{-\frac{1}{2}} = I - D^{-\frac{1}{2}} W D^{-\frac{1}{2}} $$




  • Problems with Harmonic solution
위의 Harmonic Solution은 여전히 $y_l$값은 고정한다는 조건이 있다. 이 제약조건으로 인해 문제가 발생할 수 있는데, Noise나 Outlier와 같은 문제로 인해서 하나의 label이라도 잘못되었다면 위 Model은 이 상황을 잘 대처할 수 없다. 

우리가 원하는 것은 주어진 label과 다르게 예측하더라도 Flexible하게 대처가 가능한 Model이다.

Model을 새롭게 정의해보자. 
▶ Allow $f(X_l)$ to be different from $y_l$ but penalize it
▶ Introduce a balance between labeled data fit and graph energy
$$\min_{f} \sum_{i=1}^l (f(x_i) - y_i)^2 + \lambda \mathbf{f}^T \Delta \mathbf{f}$$
$f(X_l)$이 $y_l$과 다른 값을 가질 수 있도록 $\infty$를 제거하고, 그 대신 다르다면 penalty를 준다. 이때 Hyperparameter $\lambda$를 사용하여 penalty의 trade-off를 조정한다.


위 조건식을 아래와 같이 행렬식으로 표현가능하다.
$$\min_{f} (\mathbf{f}-\mathbf{y})^T(\mathbf{f}-\mathbf{y}) + \lambda \mathbf{f}^T \Delta \mathbf{f}$$
$$\mathbf{y} = \begin{bmatrix} \mathbf{y}_l\; ; & 0 &\cdots & 0 \end{bmatrix} $$
$\mathbf{y}$는 labeled data에 대해서는 label 값을, unlabeled data에 대해서는 0값을 가진다.


이때 최적해의 미분값은 0임을 이용해 solution을 구해보자.
$$\frac{\partial E} {\partial \mathbf{f}} = (\mathbf{f}-\mathbf{y}) + \lambda \Delta \mathbf{f} = 0$$
※ Vector 미분 : $\frac{\partial (\mathbf{x} - \mathbf{s})^T W (\mathbf{x} - \mathbf{s})}{\partial \mathbf{x} } = 2W(\mathbf{x} - \mathbf{s}) $
  • Solution
$$(I+\lambda \Delta) \mathbf{f} = \mathbf{y} \;\; \Rightarrow \;\; \mathbf{f}= (I+\lambda \Delta)^{-1} \mathbf{y} $$


만약 $\lambda$가 크다면, $\lambda \Delta$의 영향이 커진다. 따라서 $y_l$의 label을 일부 바꾸더라도 model의 Smoothness에 초점을 맞춘다. 

반면 $\lambda$가 작다면, $\lambda \Delta$의 영향이 작아진다. 따라서 $y_l$의 label을 정확하게 지키는 것이 초점을 맞춘다. 



엄밀히 말하자면 Graph-based SSL은 Semi-Supervised Learning 보다는 Transductive Learning에 가깝다. 왜냐하면, 새로운 test data $x_{new}$가 주어졌을 때 바로 model에 적용할 수 없고, $x_{new}$를 포함하는 새로운 그래프를 구성하여 새롭게 Solution을 구해야 하기 때문이다.



Exemples

다음 예시를 보자.
$\mathbf{f}= (I+\lambda \Delta)^{-1} \mathbf{y}$에 대하여 $|\mathbf{f}_u|$ 값이 일정 threshold를 넘으면 해당 instance를 labeling 한다. 넘지 않으면 계속 unlabel된 상태로 유지한다. 
(만약 Threshold가 0.7이라면 $|\mathbf{f}_u| > 0.7$인 instance들 만을 labeling 한다)

그리고 갱신된 data에 대하여 다시 Graph를 구성하고 solution을 구한다. 이러한 iteration을 반복하는 모습이 위의 진행과정으로 나타난다.



  • Colliding Two moons
Graph based SSL이 잘 분류하지 못한다고 공격받는 예시가 있다. 아래와 같은 두개의 함수가 겹쳐있는 모양이다.
그런데 이러한 데이터를 잘 분류 가능한 모델이 잘 없다는 점을 생각해보면, 이러한 데이터를 잘 분류하지 못하는 것은 비단 Graph based SSL만의 문제는 아니다.



※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 정리하고, 공부한 내용을 추가하여 작성되었습니다.



댓글

댓글 쓰기

이 블로그의 인기 게시물

One-Class SVM & SVDD

-
이미지
03_6 : Anomaly Detection : Auto-Encoder, 1-SVM, SVDD MoG와 같은 밀도기반 방법론들은 특정 객체가 정상범주에 속할 확률을 구했다. 반면 Support vector 기반 방법론들은 normal과 abnormal을 구분하는 분류경계면을 찾는다. 이번 글에서는 Support vector 기반의 Anomaly detection 방법 중 one-class SVM과 SVDD를 알아보자. One-class Support Vector Machine (1-SVM, OCSVM) 1-SVM의 목표는 Data를 feature space로 mapping 한 뒤, 분류경계면을 통해 mapping된 Data 중 normal data들이 원점으로부터 최대한 멀어지게 만드는 것이다. 위 그림에서 파란색 분류경계면이 (+1) normal data들을 구분하는 것을 확인할 수 있다. 이 목표를 수식화 한 Optimization problem부터 살펴보자. Optimization Problem $$\min_{\textbf{w}}\;\;\;\frac{1}{2}||\textbf{w}||^2 + \frac{1}{\nu l} \sum_{i=1}^l \xi_i - \rho$$ $$s.t.\;\;\;\textbf{w}\cdot \Phi (x_i) \geq \rho - \xi_i\;\;\;\;(i=1,2,\cdots,l),\;\;\xi_i\geq 0$$ $\frac{1}{2}||\textbf{w}||^2$ term은 SVR과 같이 $x$의 변화에 따른 변동이 크지 않도록 Regularization을 하는 term이다. $\rho$는 위 그림에서 주황 직선을 나타내는데, 원점과 분류경계면 Hyperplane과의 거리를 나타낸다. 이 값을 뺌으로써 최소화 문제를 만족하는 최적해일때 $\rho$가 최대가 되도록 한다. (원점에서 Hyperplane이 최대한 멀어지게 만든다) $\frac{1}{\nu l} \sum_{i=1}^l \xi_i$ term은 제약식에 따라 Hyp...
자세한 내용 보기

Support Vector Regression (SVR)

-
이미지
02_4 : Kernel based learning : Support Vector Regression (SVR) 앞에서 공부했던 SVM은 binary classification을 하기 위한 방법이었다. 이번 글에서 알아볼 SVR은 함수를 추정하여 연속적인 수치변수를 예측하는 회귀 방법이다.  SVR을 알아보기에 앞서 우리가 하려는 함수추정의 목적을 살펴보자. Fitting function 함수를 추정하고 싶을 때 우리의 목적은 크게 2가지로 나뉜다. Minimize an error measure (Loss function) 한마디로 error를 최소화 하여야 한다. (잘 맞춰야 한다) Function to be simple 같은 성능이라면, 함수는 최대한 단순해야 한다. 함수가 단순하다는 뜻은 아래의 조건들을 의미한다. Fewest basis functions Simplest basis functions Flatness is desirable Support Vector Regression (SVR) 위에서 살펴보았던 Loss function과 Flatness를 반영하도록 목적함수를 만들 것이다. SVR에도 여러 종류가 있는데, 우선 $\varepsilon$-SVR에 대하여 알아보자. 현실의 Data들은 어쩔 수 없이 발생하는 noise가 존재한다. 아래 식에서 noise는 $\varepsilon$이다. $$y = f(x)+\varepsilon$$ $\varepsilon$-SVR에서 핵심 아이디어는 $\varepsilon$ 보다 작은 noise에 대해서는 Loss를 주지 말자는 것이다.  왼쪽 그림에서 색이 칠해진 영역을 Epsilon-tube 라고 하는데, 이 영역안에 있는 객체들에게는 Loss를 부여하지 않는다. 이를 위한 Loss function은 오른쪽에 표현된다. 이 Loss function은 hinge를 닮았다고 해서, Hinge Loss 라고 불린다. 차이가 $\varepsilon$ 보다 작은 경우 loss는 0이고, $\vareps...
자세한 내용 보기

Self-Training & Co-Training

-
이미지
 05_2 : Semi-Supervised Learning : Self-Training and Co-Training 우선 가장 기본적인 준지도학습 방법 Self-Training에 대하여 알아보자.  Self-Training 우리에게 주어진 정보는 Labeled data $(\mathbf{X}_l,y_l)$과 Unlabeled data $\mathbf{X}_u$이다. Self-training과정은 다음과 같이 진행된다.  1. 우선 주어진 Labeled data $(\mathbf{X}_l,y_l)$를 사용하여 예측함수 $f$를 학습시킨다. $$y_l = f(x_l)$$ 2. 학습이 완료되면, 예측함수 $f$를 사용해 Unlabeled data $\mathbf{X}_u$의 예측값 $\hat{y}_u$를 구한다. $$\hat{y}_u = f(x_u)$$ $$\Downarrow$$ 3. 이제 기존의 Labeled data와 예측함수에 의해 labeling이 된 Unlabeled data를 합치고, 이 data를 사용해 예측함수 $g$를 학습한다. 이때 어떻게 Unlabeled data를 합치는지에 따라서 많은 variation이 있다. 대표적으로 Add all $(x_u,\hat{y}_u)$ to labeled data Add a few most confident $(x_u,\hat{y}_u)$ to labeled data Add all $(x_u,\hat{y}_u)$ to labeled data, weight each by confidence. 모든 Unlabeled data를 합치는 방법, 몇몇개의 가장 예측 confidence가 높은 data만을 합치는 방법, 모든 data를 합치치만 예측 confidence에 따라서 weight를 지정하는 방법 등이 있다. 4. 위와 같은 과정을 Unlabeled data가 없어지거나, 수렴할 때 까지 반복한다. Propagating 1-Nearest Neighbor 다른 예시로 Propagating ...
자세한 내용 보기