yupsung Computer Science blog

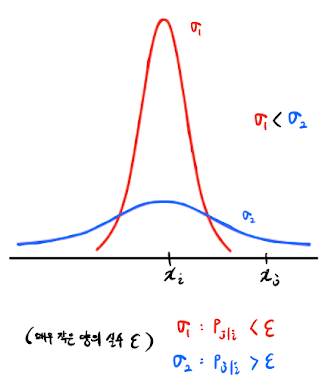
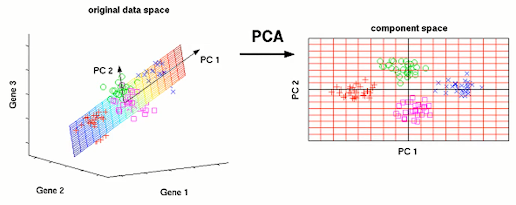
01_7 : Dimensionality Reduction : t-SNE Introduction t-SNE는 최근 가장 많이 사용되는 비선형 차원축소 방법으로써 데이터의 시각화에도 자주 사용된다. t-SNE에 대하여 알아보기에 앞서, 그 기반이 되는 Stochastic Neighbor Embedding(SNE)에 대하여 알아보자. Stochastic Neighbor Embedding (SNE) 이란? non-local distance를 보존하는 것 보다, local distance를 보존하는 것이 더 중요하다. Local distance를 최대한 보존할 수 있도록 새로운 좌표계를 만드는 것이 LLE와 SNE의 목표이다.  SNE은 LLE와 유사하지만, neighbor를 선택하는 방법에서 차이점이 있다. LLE가 Deterministic(결정론적인)한 방법을 사용한 반면, SNE는 Stochastic(확률론적인)방법을 사용한다. 기존의 LLE에서는 Deterministic하게 가장 가까운 k개의 neighbor를 선택하여 그 local distance를 보존하도록 하였다. SNE는 LLE와 다르게 Probabilistic하게 neighbor를 선택하고, 각 pairwise local distance를 보존한다. 즉, 각각의 pairwise distance가 local인지 non-local인지 확률적으로 결정한다. SNE에서 하나의 data point가 다른 data point를 neighbor로 선택할 확률을 어떻게 나타내는지 알아보자. $i$라는 data point를 기준으로, high dimension(원본 Data의 차원)과 low dimension(차원 축소한 Data의 차원)으로 나누어 생각해보자. Probability of picking $j$ given in high D  원본 Data (차원 $d$)에서 객체 $i$가 $j$를 이웃으로 선택할 확률 $$p_{j|i} = \frac{e^{-\frac{||x_i-x_j||^2}{2\sig...

01_6 : Dimensionality Reduction : ISOMAP & LLE  Locally Linear Embedding(LLE) LLE는 eigenvector를 사용한 nonlinear dimensionality reduction 방법으로써, 아래와 같은 특징이 있다. 구현하기가 쉽다. Local minima에 빠지지 않는다. (즉, 반드시 Global minima를 찾는다) highly nonlinear embedding또한 찾아낼 수 있다. 고차원의 data를 원하는 차원의 저차원으로 바꿀 수 있다. LLE Procesure Step1 : 각 Data point $x_i$에 대하여 K개의 이웃(neighbor)을 구한다. (K는 Hyperparameter) Step2 : 각 Data point를 neighbor $x_j$에 대하여 reconstruct하는데 가장 적합한 $W_ij$를 찾는다. (Cost function을 최소화 하는 $W_ij$) 아래의 그림을 예시로 생각해보자. 각 Data point $x_i$에 대하여 neighbor $x_j$들을 통해 reconstruct 하고자 한다. 이러한 과정은 아래 수식으로 표현된다. $$ E(W)=\sum_i\left| x_i - \sum_j W_{ij}x_j \right|^2 $$ $$s.t.\; W_{ij} = 0\;if\;x_j\;does\;not\;belong\;to\;the\;neighbor\;of\;x_i$$ $$\sum_j W_{ij} = 1\;for\;all\;i$$ 위의 예시에서 $x_i$는 주변의 neighbor로 구성되는 Convex Hull에 포함되고, neighbor로 부터 완벽하게 reconstruct 될 수 있다. 따라서 이 경우 $E(W) = 0$일 것이다. 반면 아래의 예시에서 $x_i$는 주변의 neighbor로 구성되는 Convex Hull에 포함되지 않고, neighbor로 부터 완벽하게 reconstruct 될 수 없다. neighbor로 부터...

01_4 : Dimensionality Reduction : Principal Component Analysis (PCA) Principal Component Analysis (PCA) 란? 지금까지 소개한 차원 축소 방법들은 Feature selection 방법으로써, 기존의 변수 중 사용할 변수를 선택하는 알고리즘이었다. 지금부터 알아볼 PCA는 Feature Extraction 방법으로써, Data가 가지고 있는 속성을 최대한으로 표현 가능한 새로운 변수 집합을 생성한다. PCA의 목표는 Original data의 분산을 최대화 하는 직교 기저(Orthogonal bases) 집합을 찾는 것이다. $$Var(X) (X\in R^3) \Rightarrow maximize\;Var(X^\prime) (X^\prime \in R^2)$$ 즉, PCA가 보존하고자 하느 특성은 Data의 분산(Variance)이다. 이러한 분산의 보존을 위하여 어떤 기저(Basis)가 선호될까? 각 직선이 데이터가 사영(Projection)되는 기저일때, 어느 기저가 선호될까? 이 경우, 오른쪽의 기저에 사영된 Data의 분산이 더 크기 때문에 오른쪽 기저가 더 선호될 것이다. PCA의 목적 (Purpose) 기저(Basis)에 사영된 data의 분산(Variance)를 최대한 보존하는 기저의 집합을 찾는 것이 목표이다. $X_1,X_2,\cdots ,X_p$ : Original variables $a_i = \{a_{i1,},a_{i2},\cdots,a_{ip}\}$ : $i\;th$ Basis/Principal Component $Y_1,Y_2,\cdots,Y_p$ : Variables after the projection onto the Basis $$Y_j=a_j^{\prime} X = a_{j1}X_1+a_{j2}X_2+\cdots+a_{jp}X_p$$ 그렇다면, 어느정도의 분산이 보존되었는지 어떻게 계산할 수 있을까? 계산에 앞서 PCA에 사용되는 개념들을 먼저 알아보...

01_3 : Dimensionality Reduction : Genetic Algorithm Meta-Heuristic Approach 매우 복잡한 문제들을  효율적  으로 Trials and Error 방법을 통해 해결한다. 자연에서 발견되는 방법들을 응용하는 경우가 많다. (ex. Neural Network, Ant Colony Algorithm, Particle Swarm Optimization) "Genetic Algorithm is an Evolutionary Algorithm that mimics the Reprodustion of Creatures" Genetic Algorithm은 유전과 진화를 모방하여 Reproduction과정을 반복하고 이를 통해 Superior Solution을 찾습니다. Selection : Quality를 향상시키는 더 좋은 해(Superior Solution)를 선택합니다. Crossover : 현재의 해들을 다양하게 조합하여 더 나은 대안을 찾습니다. Mutation : Local Optima에 빠지는 것을 방지하기 위해서 돌연변이를 발생시킵니다. Genetic Algorithm의 변수 선택과정 (Feature Selection) Initiation : 염색체 초기화 및 파라미터 설정 Fitness : 각 염색체별로 대응하는 변수를 사용하여 모델을 학습시킨다. Selection : 각각의 학습한 모델을 통해 각 염색체의 적합도 평가를 한다. Mating(Crossover) : 적합도 평가를 통해 선택된 염색체들을 통해 새로운 세대를 생성한다. Mutation : 새로운 세대들에 대하여 돌연변이를 발생시킨다. (2번으로 돌아가 과정을 반복한다) Final Generation : 5까지의 수행결과가 수렴한다면 최종적으로 해당 염색체를 선택한다. 유전 알고리즘은 변수 선택에만 사용되는 것이 아니라, 다양한 최적화 문제에 사용됩니다. 이 글에서는 변수 선택에 사용되는 유전 알고리즘을 기반으로 설명하겠습니다...

위 글들은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 통해 Machine Learning을 공부하면서 정리한 글이다. 각 글의 위 부분에 참고한 강의 영상 제목을 적어놓았다. 차원 축소란? 머신러닝을 수행하는 과정은 크게 3단계로 나누어진다. 1. Pre-Processing (전처리) 2. Learning (학습) 3. Error Analysis (오차분석) data를 전처리(Pre-processing) 하는 방법은 크게 3가지가 있는데, 대표적으로 Normalization(정규화)와 Dimension Reduction(차원 축소)가 있다. 이 글에서는 차원 축소에 대해 알아보도록 하겠다.     차원 축소의 목적 원래 가지고 있던 데이터의 변수의 개수를 줄여서 학습의 속도를 빠르게 하고 비용을 줄이는 것이다. 동시에 예측 모형의 성능저하가 최대한 일어나지 않도록 해야 할 것이다.  요약 : 모델에 가장 적합한 변수들의 부분 집합을 찾는 것   차원축소를 해야하는 이유 높은 차원을 가지는 data가 증가하여, 차원축소를 하지 않고서는 data를 사용하는 것이 불가능하거나 매우 어렵기 때문이다.   차원의 저주 (Curse of dimensionality) 동일한 설명(표현)을 위해서, 변수(variables)의 개수가 선형적으로 증가한다면 객체(sample)의 개수는 지수적으로 증가하여야 한다. 즉, n 차원의 정보를 손실 없이 표현하기 위해서는 $2^n$ 개의 sample이 필요하다. "If there are various logical ways to explain a certain phenomenon, the simplest is the best"-Occam's Razor   변수가 많아지는 경우 생기는 문제점 1. data에 noise가 포함될 확률이 높아진다. $\rightarrow$ 성능을 저하시킨다. 2. 학습과 실제 Applying에 있어서 computation burden(계...