Principal Component Analysis (PCA)
01_4 : Dimensionality Reduction : Principal Component Analysis (PCA)
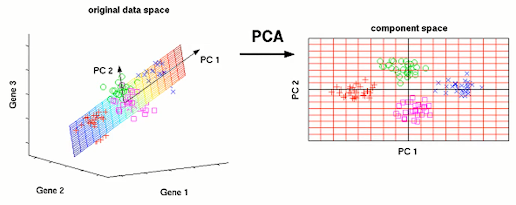
Principal Component Analysis (PCA) 란?
지금까지 소개한 차원 축소 방법들은 Feature selection 방법으로써, 기존의 변수 중 사용할 변수를 선택하는 알고리즘이었다. 지금부터 알아볼 PCA는 Feature Extraction 방법으로써, Data가 가지고 있는 속성을 최대한으로 표현 가능한 새로운 변수 집합을 생성한다.PCA의 목표는 Original data의 분산을 최대화 하는 직교 기저(Orthogonal bases) 집합을 찾는 것이다.
즉, PCA가 보존하고자 하느 특성은 Data의 분산(Variance)이다.
이러한 분산의 보존을 위하여 어떤 기저(Basis)가 선호될까?
이러한 분산의 보존을 위하여 어떤 기저(Basis)가 선호될까?
이 경우, 오른쪽의 기저에 사영된 Data의 분산이 더 크기 때문에 오른쪽 기저가 더 선호될 것이다.
PCA의 목적 (Purpose)
기저(Basis)에 사영된 data의 분산(Variance)를 최대한 보존하는 기저의 집합을 찾는 것이 목표이다.- $X_1,X_2,\cdots ,X_p$ : Original variables
- $a_i = \{a_{i1,},a_{i2},\cdots,a_{ip}\}$ : $i\;th$ Basis/Principal Component
- $Y_1,Y_2,\cdots,Y_p$ : Variables after the projection onto the Basis
그렇다면, 어느정도의 분산이 보존되었는지 어떻게 계산할 수 있을까?
계산에 앞서 PCA에 사용되는 개념들을 먼저 알아보자.
Covariance Matrix (공분산 행렬)
- $X$ : a data set (d by n matrix, d=# of variables, n=#of records)
Covariance Matrix의 계산식은 아래와 같다. $\bar{X}$는 각 vector(record)의 평균을 계산하여 행렬의 원소로 사용한 행렬이다.
$$ Cov(X) = \frac{1}{n} (X-\bar{X})(X-\bar{X})^T $$
$(X-\bar{X})$는 원래 $X$와 같이 b by n matrix이고, $(X-\bar{X})^T$는 행렬을 Transpose 하였음으로 n by d matrix이다. 따라서 계산된 $Cov(X)$행렬은 d by d 대칭 행렬일 것이다.
Covariance Matrix의 특징은 아래와 같다.
- $Cov(X)_{ij} = Cov(X)_{ji}$ (즉, Covariance Matrix는 대칭행렬이다)
- Total variance of data = $tr(Cov(C))=Cov(X)_{11}+Cov(X)_{22}+\cdots+Cov(X)_{dd}$
Projection (사영)
p에 대하여 계산하기 위하여 직교하는 vector의 곱은 0이라는 특성을 이용해보자.$$(\vec{b}-p\vec{a})^T\vec{a} = 0$$$$\vec{b}^T\vec{a}-p\vec{a}^T\vec{a} = 0$$$$p = \frac{\vec{b}^T\vec{a}}{\vec{a}^T\vec{a}}$$$$\vec{x}=p\vec{a}=\frac{\vec{b}^T\vec{a}}{\vec{a}^T\vec{a}}\vec{a}$$이때 만약 $\vec{a}$의 크기가 1이라면 (unit vector)$$p=\vec{b}^T\vec{a} \Rightarrow \vec{x}=p\vec{a}=(\vec{b}^T\vec{a})\vec{a}$$$\vec{a}$로 Basis(Principal Component)를, $\vec{b}$로 data X를 사용한다면, $p$는 기저로 data를 사영한 스칼라(scalar) 값이 될 것이다.
Eigenvalue and eigenvector (고유값과 고유벡터)
행렬 A가 있을 때 아래의 조건을 만족하는 스칼라 값 $\lambda$를 eigenvalue, vector $x$를 eigenvector 라고 한다.$$ Ax=\lambda x \Rightarrow (A-\lambda I)x=0 $$선형변환은 어떠한 vector 에 행렬을 곱하는 연산이다. $$ \begin{equation*}\begin{bmatrix}2 & 1 \\1.5 & 2 \end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix} = \begin{bmatrix}2x_1+x_2\\1.5x_1+2x_2\end{bmatrix}\end{equation*}$$
만약 행렬 A가 non-singular(역행렬을 가지는) d by d matrix이라면, 아래의 특성을 가진다.
- d개의(Rank(A)만큼의) eigenvalue, eigenvector 쌍을 가진다.
- 각각의 eigenvector들은 다른 eigenvector들과 직교한다(Orthogonal)
- 행렬 A의 대각성분의 합은 모든 eigenvalue의 합과 같다.
PCA Procedure
이제 본격적으로 PCA의 동작 과정을 살펴보자.Step 1 : Data Centering
- data의 평균이 0이 되도록 data를 조정한다.
Step 2 : Formulate the optimization problem
vector $x$를 basis $w$에 사영(Project)한다면 그 결과는 위에서 배운대로, scalar값 $p=w^Tx$이다. (x는 unit vector)
$w^Tx$의 결과는 1 by d 행렬과 d by 1 행렬을 곱하였음으로 1 by 1 행렬이 나올 것이다.
이제 이 연산을 하나의 vector $x$에서 전체 Data인 $X$로 확장해보자.
모든 Data $X$를 basis $w$에 사영한 결과는 $w^TX$로, 1 by d 행렬일 것이다.
사영을 통해 기저를 변환한 data의 분산을 계산하기 위해 위에서 배운 $Cov(X) = \frac{1}{n} (X-\bar{X})(X-\bar{X})^T$이 수식을 사용하자.
사영된 $w^TX$ 행렬의 평균은 이미 0임으로 평균값을 빼주는 연산을 제외할 수 있다. 수식을 정리하면 아래와 같다.
$$V = \frac{1}{n} (w^TX)(w^TX)^T = \frac{1}{n} w^TXX^Tw = w^TSw$$
위 수식의 계산 결과는 1 by 1 행렬로 나타날 것이다.
$$(1\;by\;d)(d\;by\;d)(d\;by\;d)(d\;by\;1)\;\Rightarrow\;(1\;by\;1)$$
또한 위 식에서 $S$는 기존의 normalized된 data의 sample covariance matrix이다.
$$S = Cov(X) = \frac{1}{n} XX^T$$
우리의 목적은 data X를 w에 사영시키고, 이때 분산 V를 최대화 하고자 한다.
이는 곧 고정된 S에 대하여 V를 최대화 하는 w를 구하는 최적화 문제로 나타내어진다.
$$maximize\;V\;=\;maximize\; w^TSw\;\;\;s.\,t.\,w^Tw=1$$
이제 이 최적해 문제는 Lagrangian multiplier를 작용하여 풀어보자.
추가 : Lagrangian multiplier (라그랑주 승수법)
라그랑주 승수법은 제약이 있는 최적화 문제를 푸는 방법 중 하나로서, 최적화 하려는 값에 라그랑주 승수항을 더하여, 문제의 제약조건을 제거하는 방법이다.
연속 미분가능 함수 $f:\mathbb{R}^D\rightarrow\mathbb{R}$과 $g:\mathbb{R}^D\rightarrow\mathbb{R}^C$에 대하여, $g(x)=0$이라는 제약 조건이 있고, $f(x)$를 최적화 하는 문제가 있다고 가정하자. 이러한 제약 조건이 있는 최적화 문제는 아래와 같이 나타낼 수 있다.
$$F(x,y)=f(x)+y\times g(x)\;\;\;F:\mathbb{R}^{D+C}\rightarrow\mathbb{R}$$
함수 $F$의 임계점(Critical point)/정류점(Stationary point)는 오일러-라그랑주 방정식(Euler–Lagrange equation)을 사용해 찾을 수 있다. 이 방법을 통해 다음을 보일 수 있다.
- 만약 $(x,y)\in\mathbb{R}^{D+C}$가 $F$의 임계점이라면, $x$는 $g=0$으로 제약한 $f$의 임계점이다.
- 만약 $x\in\mathbb{R}^D$가 $g=0$이라는 제약 조건 상에서 $f$의 임계점이라면, $(x,y)$가 $F$의 임계점인 $y\in\mathbb{R}^C$가 존재한다.
여기서 사용되는 보조변수 $y\in\mathbb{R}^C$를 라그랑주 승수라고 한다.
최적화 이론에서는 (국소적인)극점(Extremum)을 찾는것이 목표이다. 이러한 극점들은 임계점의 부분집합임으로, 임계점을 모두 찾아 극점인지 확인한다. 우리가 라그랑주 승수법을 사용하여 하고자 하는 것이 바로 이것이다.
이제 다시 PCA로 돌아가보자.
Step 3 : Obtain the solution
우리는 $g =(w^Tw-1) = 0$이라는 제약조건 하에서 $f=w^TSw$의 최적해를 찾고자 한다.
$$maximize\; w^TSw\;\;\;s.\,t.\,w^Tw=1$$
라그랑주 승수법을 사용하면 아래의 제약조건이 없는 식으로 표현된다.
$$L=w^TSw-\lambda(w^Tw-1)$$
이제 위 식에서 극대/극소점을 찾는것이 우리의 목표이다.
만약 극대/극소점이라면 도함수가 0일 것임으로 $w$에 대하여 미분한다.
$$\frac{\partial L}{\partial w} = 0 \;\Rightarrow\;Sw-\lambda w = 0\;\Rightarrow\; (S-\lambda I)w = 0$$
위의 식에서 마지막 수식의 모양을 살펴보자. Eigenvalue, eigenvector의 정의와 같지 않은가?
그렇다. $\lambda$는 $S$의 eigenvalue이고 w는 이에 대응하는 eigenvector이다!
Step 4 : Find the base set of basis
위의 과정을 통하여 구하고자 하는 최적해는 $S$의 Eigenvector 중 있다는 사실을 알았다.
그렇다면 각 Eigenvector에 대하여 사영 이후 분산을 어떻게 구할까?
먼저 eigenvector $w_1$에 $X$를 사영한 이후 분산을 구해보자.
$$v = (w_1^TX)(w_1^TX)^T = w_1^TXX^Tw_1 = w_1^TSw_1$$
Eigenvector와 eigenvalue의 정의에 따라 위 식을 정리해보자.
$$(Since\;Sw_1=\lambda_1w_1)\;\;w_1^TSw_1=w_1^T\lambda_1w_1=\lambda_1w_1^Tw_1 = \lambda_1\;\;(w_1^Tw_1 = 1)$$
놀랍게도 eigenvector $w_1$에 사영한 X의 분산은 eigenvalue $\lambda_1$이다.
우리가 구하고 싶은 것은 분산을 최대로 하는 basis이다.
따라서 S의 eigenvector와 eigenvalue를 구하고, 내림차순으로 Sort한다.
예를들어 아래와 같이 eigenvector와 eigenvalue를 구해 Sort를 마쳤다고 생각해보자.
$$Eigenvectors=\begin{equation*}\begin{bmatrix}0.6779 & -0.7357 \\0.7352 & 0.6779 \end{bmatrix}\end{equation*}\;\;\;Eigenvalues=(1.2840,\,0.0491)$$
그렇다면 basis로 Eigenvector $w_1=\begin{equation*}\begin{bmatrix}0.6779\\0.7352\end{bmatrix}\end{equation*}$를 사용하여 data $X$를 $w_1$에 사영한 경우, 이 데이터의 분산은 해당 Eigenvector의 eigenvalue인 $\lambda_1=1.2840$일 것이다.
원본 데이터와 비교하면 $\frac{\lambda_1}{\lambda_1+\lambda_2}=\frac{1.2840}{1.2840+0.0491}\approx 0.96$으로, 약 96%의 분산이 보존되었음을 확인할 수 있다.
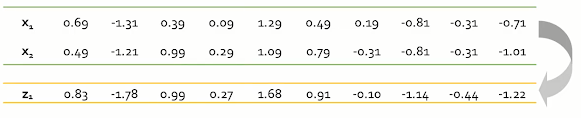
Step 5 : Extract new features
이제 분산을 최대로 보존하는 basis를 찾았으니, 해당 basis로 원본 data를 사영하여 새로운 feature를 추출한다.
Step 6 : Reconstruct the original data
사영을 통해 차원 축소된 data는 사영한 space로부터 원래의 space로 복원될 수 있다.
이러한 특징은 이후 알아볼 이상치 탐지(Anomaly detection)에서 사용된다.
PCA Issue
이제 추가적으로 PCA를 사용할 때 고려할 사항들을 알아보자.
PCA를 사용할 때 얼마나 많은 Principal Component를 사용하는것이 최적일까?
결론부터 말하자면, "그때그때 다르다" 이다. 어떤 상황에서 사용되는지, data의 구조가 어떤지 등 여러 상황에 따라서 PCA를 사용하여 몇개의 Principal Component를 추출할지는 다르다.
일반적으로 사용되는 기준으로는 정량적인 방법과 정성적인 방법이 있다.
- 정량적인 방법 : 보존되는 분산을 기준으로 정한다.
- 정성적인 방법 : 전문가의 지식을 기반으로 정한다.
우리는 여기서 정량적인 방법을 좀더 알아보도록 하자.
원본 데이터의 분산의 총량은 다음과 같다.
$$Total\;variance = \sigma_11+\sigma_22+\cdots+\sigma_dd = \lambda_1+\lambda_1+\cdots+\lambda_d$$
우리가 원본 data를 $k^{th}$ basis에 사영한다면 보존되는 분산의 양은 $\frac{\lambda_k}{\lambda_1+\lambda_2+\cdots+\lambda_d}$이다.
이제 보존되는 분산의 양을 기반으로 Principal component의 수가 증가할 때, 보존되는 분산의 양이 어떻게 변화하는지 알아보자.
그래프를 관찰하면 초반부 과정에서는 Principal component의 수가 증가할 때, 보존되는 분산의 양이 급격하게 증가함을 확인할 수 있다. 반면 과정이 진행할수록 증가하는 분산의 양이 줄어든다.
위의 그래프를 기반으로 Principal component의 개수를 선택하는 방법은 대표적으로 아래 두가지가 있다.
- Find the elbow point : 첫번째 그래프의 노란색 화살표가 가리키는 것과 같이 증가폭이 급격하게 감소하는 elbow point까지의 개수만 선택한다.
- Find the smallest PCs that preserve the predetermined required variance : 미리 지정한 목표 분산에 도달한 개수를 선택한다.
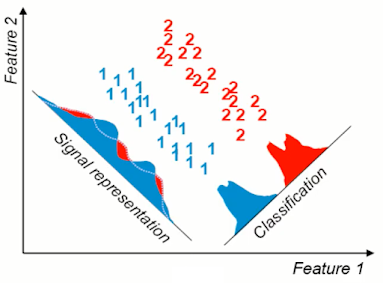
PCA Limitations
주성분 분석 방법은 통계에 기반을 두고있기 때문에 Data가 Gaussian 분포를 가진다고 가정한 방법론이다. 때문에 만약 아래의 두 번째 예시처럼 데이터가 Gaussian 분포를 가지지 않거나, 세 번째 예시처럼 Multilevel Gaussian 분포를 가진다면, 좋은 성능을 기대하기 어렵다.
그리고 Classification을 목적으로 좋은 성능을 보이기 어렵다.
아래의 예시처럼 Data가 Labeling 되어있다면, 이 data를 Classification 하기 위해서 가장 좋은 basis는 오른쪽의 basis이다. 하지만 PCA는 Data의 분산을 최대로 하는 basis를 찾기 때문에 왼쪽의 basis를 찾게된다.
※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 참고하여 작성되었습니다.
댓글
댓글 쓰기