t-SNE

01_7 : Dimensionality Reduction : t-SNE

Introduction

t-SNE는 최근 가장 많이 사용되는 비선형 차원축소 방법으로써 데이터의 시각화에도 자주 사용된다.

t-SNE에 대하여 알아보기에 앞서, 그 기반이 되는 Stochastic Neighbor Embedding(SNE)에 대하여 알아보자.

Stochastic Neighbor Embedding (SNE) 이란?

non-local distance를 보존하는 것 보다, local distance를 보존하는 것이 더 중요하다. Local distance를 최대한 보존할 수 있도록 새로운 좌표계를 만드는 것이 LLE와 SNE의 목표이다. 

SNE은 LLE와 유사하지만, neighbor를 선택하는 방법에서 차이점이 있다. LLE가 Deterministic(결정론적인)한 방법을 사용한 반면, SNE는 Stochastic(확률론적인)방법을 사용한다.

기존의 LLE에서는 Deterministic하게 가장 가까운 k개의 neighbor를 선택하여 그 local distance를 보존하도록 하였다.

SNE는 LLE와 다르게 Probabilistic하게 neighbor를 선택하고, 각 pairwise local distance를 보존한다. 즉, 각각의 pairwise distance가 local인지 non-local인지 확률적으로 결정한다.

SNE에서 하나의 data point가 다른 data point를 neighbor로 선택할 확률을 어떻게 나타내는지 알아보자. $i$라는 data point를 기준으로, high dimension(원본 Data의 차원)과 low dimension(차원 축소한 Data의 차원)으로 나누어 생각해보자.

• Probability of picking $j$ given in high D 
• 원본 Data (차원 $d$)에서 객체 $i$가 $j$를 이웃으로 선택할 확률

$$p_{j|i} = \frac{e^{-\frac{||x_i-x_j||^2}{2\sigma_i^2}}}{\sum_{k\neq i}e^{-\frac{||x_i-x_k||^2}{2\sigma_i^2}}}$$

• Probability of picking $j$ given in low D
• 차원 축소된 Data (차원 $d^\prime$)에서 객체 $i$가 $j$를 이웃으로 선택할 확률

$$q_{j|i} = \frac{e^{-||y_i-y_j||^2}}{\sum_{k\neq i}e^{-||y_i-y_k||^2}}$$

먼저 "Probability of picking $j$ given in high D" 를 살펴보자.

$$p_{j|i} = \frac{e^{-\frac{||x_i-x_j||^2}{2\sigma_i^2}}}{\sum_{k\neq i}e^{-\frac{||x_i-x_k||^2}{2\sigma_i^2}}}$$

먼저 아래의 분모는 $\sum_{j\neq i}p_{j|i} = 1$이 되도록 전체 항을 normalize하기위해 $p_{j|i}$들의 총 합으로 나누어주는 역할이다.

위의 분자를 살펴보자. 객체 $x_i$와 $x_j$가 가까울수록 $||x_i-x_j||^2$는 더 작아지고, $e$에 음수승을 취했음으로, $e^{-\frac{||x_i-x_j||^2}{2\sigma_i^2}}$는 더 커지게 된다. 따라서 가까울수록 neighbor로 선택될 확률이 증가한다.

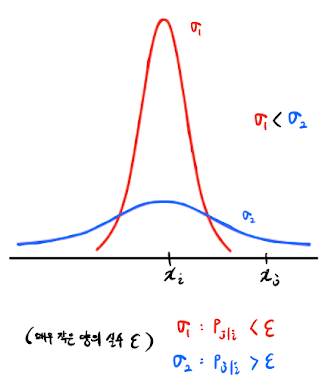
그렇다면 분자의 $\sigma_i$는 어떤 역할일까? $\sigma_i$는 $x_i$를 중점으로 하는 Gaussian 분포(정규분포)에서 Radius를 결정한다.

일반적인 data의 분포는 위치마다 밀집된 정도가 다르다. 모든 $x_i$에 대하여 동일한 radius를 사용한다면 어떤 $x_i$의 neighbor는 매우 많고, 어떤 $x_i$의 neighbor는 매우 적을 것이다. 우리는 $x_i$마다 다른 radius를 사용하여 항상 효과적인 개수의 neighbor를 선택하고자 한다. 예시를 들어보자.

위 예시에서 볼 수 있듯이 $\sigma_i$ 값이 어떤지에 따라 $x_j$가 선택될 가능성이 있거나($p_{j|i}>\epsilon$) 아예 선택되지 않는지($p_{j|i}<\epsilon$ : $\epsilon$은 매우 작은 실수임으로 이보다 확률이 작다면 사실상 선택되지 않는다)가 결정된다.

그렇다면 $\sigma_i$(radius)를 어떻게 결정해야 할까?

다행이도, SNE 논문에 따르면 SNE는 5~50 사이의 $\sigma_i$(radius)이라면, 변화에 대해서 굉장히 robust(강인)하다. 따라서 우리는 별 고민 없이 5~50 사이의 값을 선택하여 사용하거나, 일반적인 SNE 모듈에 default로 설정된 값을 사용하면 된다.

이제 Low-dimensional representation에서 사용할 Cost function을 알아볼 것이다.

그러기에 앞서 Cost function에 사용되는 Kullback-Leibler divergence (KL divergence)와 Cross Entropy개념을 먼저 짚고 넘어가자.

---

Entropy란?

KL divergence의 식을 이해하기 위해서, entropy의 개념을 이해해야 한다. Entropy개념을 정보이론의 관점에서 정립한 것은 R.V.L Hartley인데, 그의 논문에서 정보 $H$는 아래 식으로 표현된다.

$$ H = n\,\log_2{s} = \log_2{s^n}$$

왜 어떠한 정보를 표현하는데 $log$가 사용될까? 이해를 돕기 위해 예시를 생각해보자.

A는 B에게 26개 알파벳 대문자로 구성된 문자열에 대한 정보를 전달하고 싶다. A와 B 모두 전달되는 알파벳의 범주(A~Z)를 알고있을 때, 1개의 알파벳을 전달하기 위해 몇 bit가 필요할까?

정답은 $log(26)\approx 4.7$이다. 즉 최대 5 bit가 필요하다. 이렇게 적은 수의 bit만으로 전달이 가능한 이유는 A와 B 모두 Data의 범주를 알고있기 때문이다. 전달된 각 bit는 Data의 범주 [A, B, C, D, ... , Z]에서 이분탐색을 수행하는데 사용된다.

전달받은 bit가 00110이라면

[A, B, C, D, E, ... , Z] (bit 0 전달, 앞쪽 절반 선택)

[A, B, C, ... , L, M] (bit 0 전달, 앞쪽 절반 선택)

[A, B, C, ... , F] (bit 1 전달, 뒤쪽 절반 선택)

[D, E, F] (bit 1 전달, 뒤쪽 절반 선택)

[E, F] (but 0 전달, 앞쪽 절반 선택)

[E]

다음과 같이 최대 5 bit만으로 문자 1개를 전달 가능하다.

길이 n의 문자열을 전달한다고 하면, $n\,\log{26}$ 만큼의 bit가 필요할 것이다.

예시를 통해 왜 $log$로 표현되는지를 알았으니, 다시 수식을 살펴보자.

$$ H = n\,\log_2{s} = \log_2{s^n}$$

$n$은 지금 전달하려는 정보의 개수, $s$는 정보로 선택 가능한 경우의 가지수이다.

이제 이산확률 분포를 따라 어떤 정보의 경우의 선택지가 분포한다고 생각해보자.

각 사건(경우)이 발생할(선택될) 확률이 $p_i$일때 entropy는 아래와 같이 표현된다.

$$H = \sum_i p_i \log_2(\frac{1}{p_i}) = -\sum_i p_i \log_2(p_i) $$

각 사건이 발생활 확률에 대하여 최적의 전략을 사용하여 그 사건을 예측하는데 필요한 질문의 개수의 기대값이 바로 Entropy이다.

이해를 돕기위해 예시를 들어보자. 발생가능한 사건은 A, B, C, D 4가지이다.

각 사건의 발생확률이 A=0.125, B=0.25, C=0.5, D=0.125일때, 최적의 전략을 사용하여 그 사건을 예측하는데 필요한 질문의 개수는 몇번일까?

최적의 전략을 사용한다면, 사건의 발생 가능성이 가장 높은 사건부터 배제하는 것이 최적의 전략일 것이다.

1번 질문 : {C}인가? {A,B,D}인가?
2번 질문 : {B}인가? {A,D}인가?

3번 질문 : {A}인가? {D}인가?

전달한 사건이 A였다면, 총 3번의 질문으로 A라는 사실을 알아낼 수 있다.

B였다면 2번, C였다면 1번, D였다면 3번의 질문이 필요하다.

다시말해 각 사건마다 필요한 질문의 개수는 사건의 발생확률에 역수를 취하고 $log$계산을 한 결과일 것이다.

이제 각 사건마다 필요한 질문의 개수 $\log_2(\frac{1}{p_i})$에 사건의 발생확률 $p_i$를 곱한 것을 합산하면, 특정 확률분포를 가지는 상황에서 그 확률 분포의 각 사건을 표현하는데 필요한 질문의 개수의 기대값을 구할 수 있다. 이것이 그 확률 분포의 entropy이다.

확률 분포가 랜덤할수록 더 높은 entropy를 가진다. (각 사건의 발생확률이 모두 같은 경우가 최대)

---

Cross Entropy란?

이제 두 개의 확률분포 $p$와 $q$에 대해서 생각해보자. 각 확률분포마다 다른 Entropy를 가질 것이고, Entropy를 위한 최선의 전략이 다를 것이다.

만약 확률분포 $q$의 최선의 전략을 확률분포 $p$에 사용한다면 필요한 질문의 개수가 몇개일까?

Cross entropy는 어떤 문제에 대하여 특정 전략을 사용했을 때 필요한 질문개수의 기대값이다. 확률분포 $p$에 확률분포 $q$의 최선의 전략을 사용한 경우를 수식으로 표현해보자.

$$H(p,q) = \sum_i p_i \log_2(\frac{1}{q_i}) = -\sum_i p_i \log_2(q_i) $$

$i$번 사건에 대하여 $q$의 전략을 사용하면, 필요한 질문의 개수는 $\log_2(\frac{1}{q_i})$이다. 여기에 확률분포 $p$에서 $i$번 사건이 발생할 확률을 곱한 것이다.

---

Kullback-Leibler divergence (KL-divergence)

KL divergence 는 두 확률분포의 차이를 계산하기 위해 사용되는 함수이다.

Cross entropy는 확률분포 $p$에 확률분포 $q$의 전략을 사용한 경우 질문개수의 기대값이다. 이 값과 확률분포 $p$에 자기자신의 최선의 전략을 사용한 경우 질문개수의 기대값(Entropy)의 차이를 계산하면, 두 확률분포가 얼마나 차이가 나는지 계산할 수 있다.

$$KL(p||q) = H(p,q)-H(p)$$

위에서 보았던 cross entropy식에서 유도해보자.

$$\begin{align*}H(p,q) &= \sum_i p_i \log_2(\frac{1}{q_i}) = -\sum_i p_i \log_2(q_i) \\&= -\sum_i p_i \log_2(q_i) + (H(p)-(H(p)) \\&= -\sum_i p_i \log_2(q_i) - \sum_i p_i \log_2(p_i) + \sum_i p_i \log_2(q_i)\\&=- \sum_i p_i \log_2(p_i)+ \sum_i p_i \log_2(q_i) -\sum_i p_i \log_2(q_i)\\&=H(p) + \sum_i p_i \log_2(\frac{p_i}{q_i})\end{align*}$$

$$KL(p||q) = \sum_i p_i \log_2(\frac{p_i}{q_i}) = H(p,q)-H(p)$$

KL divergence는 아래의 특성을 가진다.

• $KL(p||q)\geq 0$
• $KL(p||q) \neq KL(q||p)$  (KL divergence는 거리 개념이 아니다)

이제 Cost function을 이해하기 위해 필요한 KL divergence를 알게 되었다. 다시 SNE로 돌아가보자.

---

Cost Function for a Low-dimension Representation

우리가 위에서 설명한 $p_{j|i}$와 $q_{j|i}$를 다시 상기해보자. 

$$p_{j|i} = \frac{e^{-\frac{||x_i-x_j||^2}{2\sigma_i^2}}}{\sum_{k\neq i}e^{-\frac{||x_i-x_k||^2}{2\sigma_i^2}}}$$

$$q_{j|i} = \frac{e^{-||y_i-y_j||^2}}{\sum_{k\neq i}e^{-||y_i-y_k||^2}}$$

$p_{j|i}$와 $q_{j|i}$는 아래와 같이 $x$에 대한 함수, $y$에 대한 함수로 생각할 수 있다.

$$p_{j|i} = f(x)$$

$$q_{j|i} = g(y)$$

우리는 $x$를 알고있고, $x$로 부터 $p_{j|i}$를 구할 수 있다. 우리의 목표는 $p_{j|i}$와 $q_{j|i}$의 차이를 최소로 하는 저차원의 좌표시스템 $y$를 구하는 것이다. $p_{j|i}$와 $q_{j|i}$의 차이를 어떻게 구할까? 각 확률분포의 차이를 구할 때 사용하는 방법이 KL divergence라고 위에서 공부했다. 따라서 모든 $P_i,\,Q_i$들의 차이를 KL divergence를 통해 구하고 합한 값이 Cost가 된다.

$$Cost = \sum_i KL(P_i||Q_i) = \sum_i\sum_j p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}$$

우리의 목표는 KL divergence를 통해 고차원 상에서 객체들이 neighbor를 선택할 확률분포와 동일한 객체들이 저차원 상에서 동일한 neighbor를 선택할 확률분포를 최대한 일치하도록 하는 저차원의 좌표계를 찾는 것이 목표이다. 다시 말해, 이 Cost를 최소로 만드는 $Y$를 찾는 것이다. 

KL divergence의 이해를 돕기위해 예시를 살펴보자,

확률분포 $p$와 $q$가 왼쪽의 그래프로 그려진다. 이때 두 확률분포의 KL divergence는 오른쪽 그래프의 색칠된 영역이다. 

---

Cost Function for a Low-dimension Representation (Cont.)

이제 저 Cost function을 최소화 하는 $Y$를 찾기 위해서, Cost function을 $y_i$에 대하여 편미분 해야하는데, 논문에 "Differencing Cost is tedious because $y_k$ affect $q_{ij}$ via normalized term in equation, but the result is simple" 이라는 말이 나올 정도로 이 과정이 매우 어렵다. 하지만 결과는 Simple 하다. 우선 결과는 아래와 같다.

$$Cost = C = \sum_i KL(P_i||Q_i) = \sum_i\sum_j p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}$$

$$\frac{\partial C}{\partial y_i} = 2\sum_j (y_j-y_i)(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})$$

$\frac{\partial C}{\partial y_i}$를 계산할때 $y_i$ term 이 분모에도 영향을 미치기 때문에 계산이 복잡하지만, 한번 계산해보도록 하자.

$$\begin{align*}C &= \sum_i KL(P_i||Q_i) = \sum_i\sum_j p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}\\&= \sum_i\sum_j p_{j|i} \log p_{j|i} - \sum_i\sum_j p_{j|i} \log q_{j|i}\end{align*}$$

$y_i$는 앞쪽 $p$ 항에는 영향을 주지 않음으로, $\sum_i\sum_j p_{j|i} \log p_{j|i}$를 상수로 취급해도 문제가 없다. 상수항을 제거한 $C^\prime$ 을 만들자. 그래도 편미분 결과는 $C$와 같다.

$$C^\prime = - \sum_i\sum_j p_{j|i} \log q_{j|i} \;\;\;\;\;(\frac{\partial C}{\partial y_i} = \frac{\partial C^\prime}{\partial y_i})$$

$C^\prime$에 $\sum_i\sum_j$ 부분을 임의의 $t$에 대하여 각각의 경우를 묶어준다. $t$가 앞쪽에 오는 경우 ($\sum_i p_{t|i} \log q_{t|i}$), 뒤쪽에 오는 경우 ($\sum_j p_{j|t} \log q_{j|t}$), 양쪽 모두 없는 경우 ($\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \log q_{i|j}$)로 나누어준다.

$$C^\prime =-\sum_i p_{t|i} \log q_{t|i} - \sum_j p_{j|t} \log q_{j|t} - \sum_{i\neq t}\sum_{j\neq t} p_{i|j} \log q_{i|j}$$

이 식을 쉽게 계산하기 위해서 새로운 $d_{ti}$를 정의해보자.

$$d_{ti} = \exp(-||y_t-y_i||^2)$$

$$d_{it}= \exp(-||y_i-y_t||^2)\;\;\;\;\;\;(d_{ti} = d_{it})$$

$d_{ti}$를 $y_t$에 대하여 미분해보자.

$$\frac{\partial d_{ti}}{\partial y_t} = d^{\prime}_{ti} = -2(y_t-y_i)\exp(-||y_t-y_i||^2) = -2(y_t-y_i)d_{ti}$$

$d$를 사용하여, $q_{t|i},\;q_{j|t},\;q_{i|j}$를 표현해보자.

$$q_{t|i} = \frac{\exp(-||y_i-y_t||^2)}{\sum_{k\neq i}\exp(-||y_i-y_k||^2)} = \frac{d_{it}}{\sum_{k\neq i}d_{ik}}$$

$$q_{j|t} = \frac{\exp(-||y_t-y_j||^2)}{\sum_{k\neq t}\exp(-||y_t-y_k||^2)} = \frac{d_{tj}}{\sum_{k\neq t}d_{tk}}$$

$$q_{i|j} = \frac{\exp(-||y_j-y_i||^2)}{\sum_{k\neq j}\exp(-||y_j-y_k||^2)} = \frac{d_{ji}}{\sum_{k\neq j}d_{jk}}$$

이제 $\frac{\partial C^\prime}{\partial y_t}$를 계산해보자.

$$\frac{\partial}{\partial y_t}(C^\prime) =\frac{\partial}{\partial y_t}(-\sum_i p_{t|i} \log q_{t|i}) + \frac{\partial}{\partial y_t}(-\sum_j p_{j|t} \log q_{j|t}) + \frac{\partial}{\partial y_t}(-\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \log q_{i|j})$$

각 항별로 나누어서 미분을 해보자.

• Gradient of ($-\sum_i p_{t|i} \log q_{t|i}$) term (1)

$$\begin{align*}&\frac{\partial}{\partial y_t}(-\sum_i p_{t|i} \log q_{t|i}) = -\sum_i p_{t|i} \frac{1}{q_{t|i}}\frac{\partial q_{t|i}}{\partial y_t}\\&=-\sum_i p_{t|i} \frac{1}{q_{t|i}}\frac{\partial}{\partial y_t}(\frac{d_{it}}{\sum_{k\neq i}d_{ik}})\\&=-\sum_i p_{t|i} \frac{1}{q_{t|i}}\frac{d^{\prime}_{it}(\sum_{k\neq i}d_{ik})-d_{it}d_{it}^{\prime}}{(\sum_{k\neq i}d_{ik})^2}\;\;\;\;\;\;(\frac{\partial (\sum_{k\neq i}d_{ik})}{\partial y_t} = d^{\prime}_{it})\\&=-\sum_i p_{t|i} \frac{1}{q_{t|i}}\frac{-2(y_t-y_i)d_{it}(\sum_{k\neq i}d_{ik})+2(y_t-y_i)d_{it}^2}{(\sum_{k\neq i}d_{ik})^2}\;\;\;\;\;\;(d^{\prime}_{it}=-2(y_t-y_i)d_{it})\\&=-\sum_i p_{t|i} \frac{1}{q_{t|i}}(-2(y_t-y_i)q_{t|i}+2(y_t-y_i)q_{t|i}^2)\;\;\;\;\;\;(\frac{d_{it}}{\sum_{k\neq i}d_{ik}} = q_{t|i})\\&=\sum_i 2p_{t|i} (y_t-y_i)(1-q_{t|i})\end{align*}$$

• Gradient of ($-\sum_j p_{j|t} \log q_{j|t})$) term (2)

$$\begin{align*}&\frac{\partial}{\partial y_t}(-\sum_j p_{j|t} \log q_{j|t}) = -\sum_j p_{j|t} \frac{1}{q_{j|t}}\frac{\partial q_{j|t}}{\partial y_t}\\&=-\sum_j p_{j|t} \frac{1}{q_{j|t}}\frac{\partial}{\partial y_t}(\frac{d_{tj}}{\sum_{k\neq t}d_{tk}})\\&=-\sum_j p_{j|t} \frac{1}{q_{j|t}}\frac{d_{tj}^{\prime}(\sum_{k\neq t}d_{tk})-d_{tj}(\sum_{k\neq t} d_{tk}^{\prime})}{(\sum_{k\neq t}d_{tk})^2}\\&=-\sum_j p_{j|t} \frac{1}{q_{j|t}}\frac{-2(y_t-y_j)d_{tj}(\sum_{k\neq t}d_{tk})-d_{tj}(\sum_{k\neq t} d_{tk}^{\prime})}{(\sum_{k\neq t}d_{tk})^2}\\&=2\sum_j p_{j|t} (y_t-y_j) + \sum_j p_{j|t} \frac{\sum_{k\neq t}d_{tk}^{\prime}}{\sum_{k\neq t}d_{tk}}\\&=2\sum_j p_{j|t} (y_t-y_j) + \sum_j\frac{d_{tj}^{\prime}}{\sum_{k\neq t}d_{tk}}\;\;\;\;\;\;(\sum_j p_{j|t} = 1)\\& (+ while\;\;d^{\prime}_{tt} = 0,\;\;\sum_{k\neq t}d_{tk}^{\prime} = \sum_k d_{tk}^{\prime}\;\;(notation\;\;change)\rightarrow \sum_j d_{tj}^{\prime})\\&=2\sum_j p_{j|t} (y_t-y_j) -2\sum_j(y_t-y_j)\frac{d_{tj}}{\sum_{k\neq t}d_{tk}}\;\;\;\;\;\;(d^{\prime}_{tj}= -2(y_t-y_j)d_{tj})\\&=2\sum_j p_{j|t} (y_t-y_j) -2\sum_j(y_t-y_j)q_{j|t}\;\;\;\;\;\;(\frac{d_{tj}}{\sum_{k\neq t}d_{tk}}=q_{j|t})\\&=2\sum_j (y_t-y_j)(p_{j|t} - q_{j|t})\end{align*}$$

• Gradient of ($-\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \log q_{i|j}$) term (3)

$$\begin{align*}&\frac{\partial}{\partial y_t}(-\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \log q_{i|j}) = -\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \frac{1}{q_{i|j}}\frac{\partial q_{i|j}}{\partial y_t}\\&= -\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \frac{1}{q_{i|j}}\frac{\partial}{\partial y_t}(\frac{d_{ji}}{\sum_{k\neq j}d_{jk}})\\&= -\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \frac{1}{q_{i|j}}\frac{d^{\prime}_{ji}\sum_{k\neq j}d_{jk} - d_{ji}d^{\prime}_{jt}}{(\sum_{k\neq j}d_{jk})^2}\\&= -\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \frac{1}{q_{i|j}}\frac{- d_{ji}d^{\prime}_{jt}}{(\sum_{k\neq j}d_{jk})^2}\;\;\;\;\;\;(d^{\prime}_{ji} = \frac{\partial d_{ij}}{\partial y_t} = 0)\\&= -\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \frac{1}{q_{i|j}}\frac{2(y_t-y_j)d_{ji}d_{jt}}{(\sum_{k\neq j}d_{jk})^2}\;\;\;\;\;\;(d^{\prime}_{jt} = -2(y_t-y_j)d_{jt})\\&= -\sum_{i\neq t}\sum_{j\neq t} p_{i|j} \frac{1}{q_{i|j}}\cdot 2(y_t-y_j)q_{i|j}q_{t|j}\;\;\;\;\;\;(\frac{d_{ji}}{\sum_{k\neq j}d_{jk}}=q_{i|j},\;\;\frac{d_{jt}}{\sum_{k\neq j}d_{jk}} = q_{t|j})\\&= -\sum_{i\neq t}\sum_{j\neq t} 2(y_t-y_j)p_{i|j}q_{t|j}\end{align*}$$

이제 각각 미분한 결과를 합쳐보자.

• (1) + (3)

$$\begin{align*}&\sum_i 2p_{t|i} (y_t-y_i)(1-q_{t|i})-\sum_{i\neq t}\sum_{j\neq t} 2(y_t-y_j)p_{i|j}q_{t|j}\\&=2\sum_j (y_t-y_j)p_{t|j}-2\sum_j (y_t-y_j)p_{t|j}  q_{t|j}-2\sum_{i\neq t}\sum_{j\neq t} (y_t-y_j)p_{i|j}q_{t|j}\\&=2\sum_j (y_t-y_j)p_{t|j}-2\sum_j (y_t-y_j)p_{t|j}  q_{t|j}-2\sum_{i\neq t}\sum_{j} (y_t-y_j)p_{i|j}q_{t|j}\;\;\;\;((y_t-y_t)p_{i|j}q_{t|j} = 0)\\&=2\sum_j (y_t-y_j)p_{t|j}-2\sum_{i}\sum_{j} (y_t-y_j)p_{i|j}q_{t|j}\;\;\;\;(\sum_j (y_t-y_j)p_{t|j}  q_{t|j} = \sum_{i=t}\sum_{j} (y_t-y_j)p_{i|j}q_{t|j})\\&=2\sum_j (y_t-y_j)p_{t|j}-2\sum_{j}\sum_{i} p_{i|j}(y_t-y_j)q_{t|j}\\&=2\sum_j (y_t-y_j)p_{t|j}-2\sum_{j} (y_t-y_j)q_{t|j}\;\;\;\;\;\;(\sum_i p_{i|j} = 1)\\&=2\sum_j (y_t-y_j)(p_{t|j}-q_{t|j})\end{align*}$$

• (1) + (2) + (3)

$$\begin{align*}&2\sum_j (y_t-y_j)(p_{t|j}-q_{t|j}) + 2\sum_j (y_t-y_j)(p_{j|t} - q_{j|t})\\&=2\sum_j (y_t-y_i)(p_{t|j}-q_{t|j}+p_{j|t}-q_{j|t})\end{align*}$$

이제 $\frac{\partial C^\prime}{\partial y_t}$를 구했다.

그러면 Cost function의 미분을 사용하여 Gradient를 update하는 과정은 아래의 momentum term으로 표현된다.

$$\mathcal{y}^{(t+1)} = \mathcal{y}^{(t)} + \eta \frac{\partial C}{\partial \mathcal{y}} + \alpha(t)(\mathcal{y}^{(t)}-\mathcal{y}^{(t+1)})$$

기존 SNE 논문에 기술된 수식과 약간의 차이가 있는데, 기술된 수식의 notation이 조금 달라, 자료가 반전되어 표현된다는 차이점이 있다.

• 논문

$$\frac{\partial C}{\partial y_i} = 2\sum_j (y_j-y_i)(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})$$

• 글의 수식

$$\frac{\partial C}{\partial y_t} = 2\sum_j (y_t-y_i)(p_{t|j}-q_{t|j}+p_{j|t}-q_{j|t})$$

---

Symmetric SNE 란?

지금까지 공부했던 SNE는 Symmetric하지 않다. 즉 $p_{i|j} \neq p_{j|i}$이다.

SNE를 Symmetric 하게 바꾸기 위해서 conditional probability $p_{i|j}$를 pairwise probablility로 바꿔보자.

$$p_{ij} = \frac{e^{-\frac{||x_i-x_j||^2}{2\sigma_i^2}}}{\sum_{k\neq l}e^{-\frac{||x_k-x_l||^2}{2\sigma_i^2}}}$$

$$p_{ij}=\frac{p_{i|j}+p_{j|i}}{2n},\;\;\;\;\;\;\sum_j p_{ij} > \frac{1}{2n}$$

그렇다면, Cost Function 과 Gradient는 아래와 같다. 기존의 SNE보다 좀더 식이 간단해진다.

$$Cost = \sum_i KL(P_i||Q_i) = \sum_i \sum_j p_{ij} \log \frac{p_{ij}}{q_{ij}}$$

$$\frac{\partial C}{\partial y_i} = 4 \sum_j (y_j-y_i)(p_{ij}-q_{ij})$$

하지만 Symmetric SNE에는 Crowding problem이라는 문제점이 있다.

Gaussian 분포를 사용하는 SNE의 특성상 $x_i$로 부터 가까울때는 완만하게 함수값이 감소하지만, 어느정도 적당히 멀어진다면 급격하게 함수 값이 감소하면서 SNE의 결과, 저차원 공간상의 데이터 집합이 중심에만 모이는 문제가 발생한다. 이를 Crowding problem이라고 한다.

이를 해결하기 위해 분포의 꼬리쪽 경사가 완만한, 그리고 꼬리쪽 함수값이 너무 작지 않은 t-distribution을 사용해보자.

---

t-Distributed Stochastic Neighbor Embedding (t-SNE) 이란?

위에서 설명한 Crowding problem 문제점을 해결하기 위해 저차원 공간상에서 이웃을 선택하는 기준으로 t-distribution을 사용한 SNE가 t-SNE이다.

t-distribution의 분포가 Gaussian(Z) 분포보다 더 완만히 감소하고 꼬리의 함수값이 더 크다는 점을 확인할 수 있다.

t-distribution은 다음과 같다.

$$f(t) = \frac{\Gamma(\frac{v+1}{2})}{\sqrt{v\pi}\Gamma{\frac{v}{2}}}(1+\frac{t^2}{v})^{-\frac{v+1}{2}}$$

$$\Gamma(n) = (n-1)!$$

t-distribution을 사용해 저차원에서 neighbor를 선택할 확률을 계산하면,

$$q_{ji} = \frac{1+||y_i-y_j||^2)^{-1}}{\sum_{k\neq l}(1+||y_i-y_j||^2)^{-1}}$$
이다. 고차원에서 neighbor를 선택할 확률은 기존의 Gaussian 을 사용한 $p_{ij}$를 사용한다.

Cost function은 기존의 KL-divergence를 사용한 

$$C = \sum_i KL(P_i||Q_i)= \sum_i\sum_j p_{ji} \log \frac{p_{ji}}{q_{ji}}$$

이다. 그럼 Gradient를 계산하면 아래의 결과가 나온다.

$$\frac{\partial C}{\partial y_i} = 4\sum_j (y_j-y_i)(p_{ij}-q_{ij})(1+||y_i-y_j||^2)^{-1}$$

결론적으로 t-SNE의 과정은 아래의 sudo code와 같이 진행된다.

마지막으로 MNIST data에 여러 차원축소 방법을 사용한 결과를 비교해보자.

• PCA

• ISOMAP

• t-SNE

결과를 살펴보면 PCA < ISOMAP < t-SNE 순으로 각 Class의 분류가 더 잘 수행되었음을 확인할 수 있다. 하지만 PCA < ISOMAP < t-SNE 순으로 t-SNE가 가장 시간이 오래 걸렸다는 단점도 있다.

※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 참고하여 작성되었습니다.