yupsung Computer Science blog

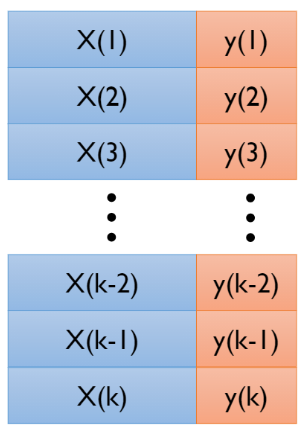
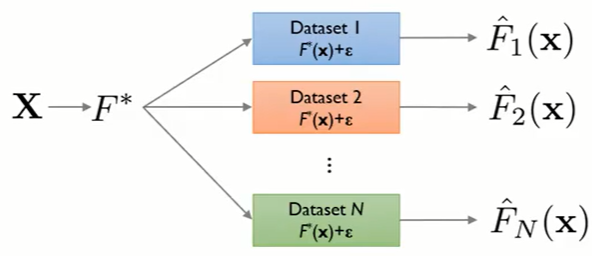
04_4 : Ensemble Learning : Random-Forests Random Forest는 이전 글에서 공부했던 Bagging 방법의 특수한 형태로써 Decision Tree를 Base Learner로 사용한다. Random 하게 변수를 선택하여 여러개의 Decision Tree들( Forest )을 학습시키는 방법을 사용한다. 우선 Decision Tree에 대하여 알아보자. Decision Tree $d$개의 변수를 가지는 Data가 주어졌다고 가정하자. 이때 하나의 data point $v$는 아래와 같이 정의된다. $$v = (x_1,x_2,\cdots ,x_d) \in \mathbb{R}^d $$ 각 $x_i$는 변수 하나하나를 나타내는 스칼라 값이다. 변수가 매우 많은 경우, 앞서 배운 차원축소와 같은 방법을 사용하거나 이후에 다룰 Random Forest처럼 임의로 변수를 추출하여 사용한다. 변수의 추출은 $\phi (v)$ 함수에 의해서 이루어진다. $$\phi\;:\;\mathbb{R}^d \rightarrow \mathbb{R}^{d^\prime},\;\;\;\;d > d^\prime$$ Training Training 단계에서는 초록색 end node에 대응하는 정답 Label($y$)을 사용하여 각 노드를 분할하는 Split function의 매개변수를 최적화 한다. 각 노드에 대응되는 Data set을 $S$라고 하자. 그렇다면, 해당 집합은 Split function에 의하여 $S^L,\;S^R$ 두개의 집합으로 분할된다.  $$S_i = S_i^L \cup S_i^R,\;\;S_i^L \cap S_i^R = \emptyset $$ 이렇게 Data를 분할하는 Split function은 데이터를 정보 획득량(information gain : $I$)이 최대화 되도록 분리한다. $$I = H(S) - \sum_{i\in\{L,R\}} \frac{|S^i|}{|S|} H(S^i),\;\;\;\;H(S) = -\sum...

 04_3 : Ensemble Learning : Bagging 앙상블 방법의 핵심은 Diversity (다양성)을 확보하는 것이다. Bagging 방법은 Implicit diversity 관점에서 Data의 다양성을 확보하려는 방법이다. 우리에게 주어진 Dataset은 하나의 큰 data 집합이다. 이 Dataset을 여러 방법으로 조절하여 다양성을 늘려보자.  K-fold data split K-fold 방법은 가장 처음 시도된 방법론이다. 딥러닝에서 Cross validation과 거의 동일한 메커니즘으로 동작한다.  우선 전체 Dataset을 K개의 subset으로 분할한다.  그리고 각 model마다 사용할 train dataset으로 대응되는 subset 1개를 제외하고 K-1개의 subset을 사용한다. 예를들어 2번째 model $f_2$가 사용할 train dataset으로는 k-1번째 subset이 제외된 나머지 dataset이 사용된다. 모든 모델의 학습이 완료되면 aggregation function $\delta(\cdot )$을 사용하여 결과를 구한다. $$ \hat{y} = \delta \big( f_1(x), f_2(x), \cdots, f_k(x)\big) $$ 서로 다른 train dataset을 사용하였으니, $f_1 \neq f_2 \neq \cdots \neq f_k$ 이다. 하지만 개별 model들이 완전히 독립적이지 않다는 문제점이 있다. 왜냐하면, 항상 임의의 $f_i$와 $f_j$는 $k-2$개의 fold를 공유하기 때문이다. 또한 데이터를 subset으로 나누는데 한계가 있다. 그렇기 때문에 K-fold방법으로 생성가능한 train dataset의 개수에도 한계가 있다. K-fold data split은 위와 같은 단점 때문에 요즘에는 잘 쓰이지 않는 방법이다. Bootstrap Aggregating (Bagging) Data Sampling Bagging 방법은 $N$개의 Ori...

04_2 : Ensemble Learning : Bias-Variance Decomposition 이번 글에서는 Ensemble learning의 이론적 Background로 필요한 Bias-Variance Decomposition을 알아보고, 수학적으로 앙상블 기법을 사용하는 것이 왜 좋은지 증명해 보도록 하자. Bias-Variance Decomposition 데이터가 Additive error model로 부터 생성된다고 가정하자. $$y = F^*(x) + \epsilon,\;\;\;\epsilon \sim N(0,\sigma^2) $$ $F^*$는 target function이다. 우리가 모르기 때문에 학습을 통해 추측하려 한다. Error $\epsilon$은 independent and identically distributed (iid) 즉, 상호 독립적이고 동일한 정규분포 $N$을 따른다고 가정하자. 우리는 각각의 학습 Dataset을 통해 여러개의 Model을 추정할 것이다. 추정한 함수를 $\widehat{F}_N(x)$라고 하자. 추정을 반복했을 때 그 함수의 기대값을 $\overline{F}(x)$라고 한다. $$\overline{F}(x) = E\big[\widehat{F}_D(x)\big]$$ 이제 특정 data point $x_0$에 대하여 Mean Squared Error가 어떻게 계산되는지 살펴보고, 여기서 Bias-Variance Decomposition을 유도해보자. $$\begin{align*}Err(x_0) &= E\big[y-\widehat{F}(x) | x=x_0 \big]^2\\&=E\big[(F^*(x_0)+\epsilon)-\widehat{F}(x_0) \big]^2\;\;\;\;\;(y = F^*(x)+\epsilon)\\&=E\big[F^*(x_0)-\widehat{F}(x_0)+\epsilon\big]^2\end{align*}$$ 제곱항을 풀기 위해서 $F^*(x_0)-\widehat{...

04_1 : Ensemble Learning : Overview 이번 글에서는 간략하게 Ensemble 기법이 어떤 것인지, 왜 사용하는지 알아보도록 하자. Backgrounds 위의 예시는 여러 종류의 데이터 셋에 대하여 각 Classification 알고리즘들이 얼만큼의 성능을 보이는지 Error율을 기반으로 표현한 그래프이다. 그래프를 보면, 모든 데이터 셋에 대하여 우월한 성능을 보이는 알고리즘은 없는 것을 확인할 수 있다. 각 데이터 셋의 특성에 따라 더 좋은 알고리즘이 그때 그때 다르다. 그렇다면 다른 모든 알고리즘들 보다 우월한, 모든 데이터 종류에 대하여 항상 좋은 성능을 보이는 알고리즘은 존재하지 않는걸까? No Free Lunch Theorem "공짜 점심은 없다"는 이 이론에 따르면, 그런 알고리즘은 존재하지 않는다. 정확히는 어떤 알고리즘도 모든 상황에서 다른 알고리즘보다 우월하다는 결론을 내릴 수 없다. 이 이론을 설명하는 논문에 제시된 결론은 다음과 같다. 좋은 일반화 성능을 원한다면, Context-independent 하거나 Usage-independent 한 이유로 한 알고리즘을 선호할 수 없다. (다시 말해, 항상 Context와 사용할 용도를 고려하여 알고리즘을 선택해야 한다는 뜻이다) 만약 한 알고리즘이 다른 알고리즘들에 비해 좋은 성능을 보인다면, 그것은 그 알고리즘이 해당 데이터 셋의 특성과, 용도에 적합하기 때문이다. 때문에 우리는 엄청난 알고리즘 하나만을 여기저기 사용하여 공짜 점심을 먹으려 날로먹으려 하지 말고, 사용할 용도와 Data의 특성, Context, 경험적인 지식, 통계적인 정보 등 여러 지표를 종합적으로 고려하여 적절한 알고리즘을 선택해야 한다. 그런데 No Free Lunch 이론을 제시한 논문에서, 추가적으로 아래와 같은 실험 결과를 제시하였다. " However, if they are properly combined ...  Every ensemble method com...

03_6 : Anomaly Detection : Auto-Encoder, 1-SVM, SVDD MoG와 같은 밀도기반 방법론들은 특정 객체가 정상범주에 속할 확률을 구했다. 반면 Support vector 기반 방법론들은 normal과 abnormal을 구분하는 분류경계면을 찾는다. 이번 글에서는 Support vector 기반의 Anomaly detection 방법 중 one-class SVM과 SVDD를 알아보자. One-class Support Vector Machine (1-SVM, OCSVM) 1-SVM의 목표는 Data를 feature space로 mapping 한 뒤, 분류경계면을 통해 mapping된 Data 중 normal data들이 원점으로부터 최대한 멀어지게 만드는 것이다. 위 그림에서 파란색 분류경계면이 (+1) normal data들을 구분하는 것을 확인할 수 있다. 이 목표를 수식화 한 Optimization problem부터 살펴보자. Optimization Problem $$\min_{\textbf{w}}\;\;\;\frac{1}{2}||\textbf{w}||^2 + \frac{1}{\nu l} \sum_{i=1}^l \xi_i - \rho$$ $$s.t.\;\;\;\textbf{w}\cdot \Phi (x_i) \geq \rho - \xi_i\;\;\;\;(i=1,2,\cdots,l),\;\;\xi_i\geq 0$$ $\frac{1}{2}||\textbf{w}||^2$ term은 SVR과 같이 $x$의 변화에 따른 변동이 크지 않도록 Regularization을 하는 term이다. $\rho$는 위 그림에서 주황 직선을 나타내는데, 원점과 분류경계면 Hyperplane과의 거리를 나타낸다. 이 값을 뺌으로써 최소화 문제를 만족하는 최적해일때 $\rho$가 최대가 되도록 한다. (원점에서 Hyperplane이 최대한 멀어지게 만든다) $\frac{1}{\nu l} \sum_{i=1}^l \xi_i$ term은 제약식에 따라 Hyp...

03_6 : Anomaly Detection : Auto-Encoder, 1-SVM, SVDD Auto encoder 자체는 다양한 분야에 활용되는 모델이다. 이 글에서는 간단하게 어떤식으로 이상치 탐지에 이용되는지 알아볼 것이다. Auto Encoder (Auto-Associative Neural Network) 이미지를 처리하는 경우 Convolutional Auto Encoder를, 시계열이나 자연어와 같은 데이터를 처리하는 경우 RNN 기반의 Auto Encoder를 사용하는 등 다양한 응용이 있다. 하지만 이 글에서는 가장 기본적인 Feed-forward neural network에서 Auto Encoder를 이해해보자. Auto Encoder의 목적은 입력으로 주어진 data를 출력으로 최대한 원본에 가깝게 reproduce 하는 것이다. 목적함수인 Loss function을 살펴보자. Loss function $$l(f(x)) = \frac{1}{2}\sum_k(\hat{x}_k-x_k)^2$$ 입력값 $x_k$와 reproduce 한 $\hat{x}_k$의 차이가 loss function이다. Encoder $$h(x) = g(a(x)) = sigmoid(b+Wx)$$ activation function으로 Sigmoid 함수를 사용한 예시이다. 입력 $x\in R^D$를 $h(x)\in R^d$로 인코딩한다. 이때 반드시 $d<D$이어야 한다. 왜냐하면 인코딩 과정에서 정보의 축약(손실)이 일어나야지만 입력 data의 특징을 잘 보존하는 hidden layer를 학습할 것이고, 이를 통해 이상치 탐지를 할 수 있기 때문이다. (이후에 좀더 자세히 알아보자) + hidden layer를 latent vector라고 부르기도 한다. Decode $$\hat{x} = o(\hat{a}(x)) = sigmoid(c+W^*h(x))$$ Encoding된 $h(x)$를 다시 원래 차원의 data $\hat{x}$로 복원하는 과정이다. 여기서...

 03_2 : Anomaly Detection : (Mixture of) Gaussian Density Estimation 이전까지 normal data가 하나의 가우시안 분포로 부터 생성된다고 가정하였다. 하지만 하나의 가우시안만을 사용하는 것은 너무 엄격하다.( Strong model : uni-modal and convex ) 때문에 여러개의 가우시안 분포의 혼합( multi-modal )을 사용하여 설명하려고 한다. Mixture of Gaussian (MoG) Density Estimation Mixture of Gaussian(MoG)는 여러개의 가우시안 분포의 선형 결합으로 이루어진다. 덕분에 이전의 하나의 가우시안을 사용하는 경우보다 더 bias가 적게 추정이 가능하다. 하지만 좀 더 많은 Training data를 필요로 한다. $$f(x) = w_1N(\mu_1,\sigma_1^2) + w_2N(\mu_2,\sigma_2^2) + w_3N(\mu_3,\sigma_3^2)$$ 이전의 방법에서는 $\mu$와 $\sigma$ 2개의 미지수를 추정하면 되었지만, $K$개의 가우시안을 혼합하는 MoG의 경우에는 각 가우시안 마다 $w_i,\,\mu_i,\,\sigma_i$ 3개씩 총 $3K$개의 미지수, 그리고 몇개의 가우시안을 사용할지 $K$까지 학습을 통해 추정해야 한다. Components of MoG Probability of an instance belonging to the normal class $$p(x|\lambda) = \sum_{m=1}^M w_m g(x|\mu_m,\Sigma_m)$$ $$\lambda = \{w_m,\mu_m,\Sigma_m\},\;\;\;\;\;m=1,\cdots,M$$ Distribution of each Gaussian model $$g(x|\mu_m,\Sigma_m) = \frac{1}{(2\pi)^{d/2}|\Sigma_m|^{1/2}}\exp{\big[\frac{1}{2}(x-\mu_m)^T\S...