Bias-Variance Decomposition
04_2 : Ensemble Learning : Bias-Variance Decomposition
이번 글에서는 Ensemble learning의 이론적 Background로 필요한 Bias-Variance Decomposition을 알아보고, 수학적으로 앙상블 기법을 사용하는 것이 왜 좋은지 증명해 보도록 하자.
Bias-Variance Decomposition
데이터가 Additive error model로 부터 생성된다고 가정하자.
$$y = F^*(x) + \epsilon,\;\;\;\epsilon \sim N(0,\sigma^2) $$
$F^*$는 target function이다. 우리가 모르기 때문에 학습을 통해 추측하려 한다.
Error $\epsilon$은 independent and identically distributed (iid) 즉, 상호 독립적이고 동일한 정규분포 $N$을 따른다고 가정하자.
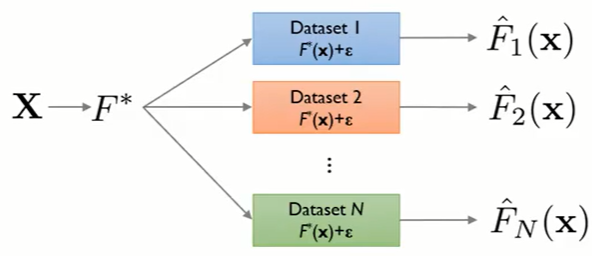
우리는 각각의 학습 Dataset을 통해 여러개의 Model을 추정할 것이다. 추정한 함수를 $\widehat{F}_N(x)$라고 하자. 추정을 반복했을 때 그 함수의 기대값을 $\overline{F}(x)$라고 한다.
$$\overline{F}(x) = E\big[\widehat{F}_D(x)\big]$$
이제 특정 data point $x_0$에 대하여 Mean Squared Error가 어떻게 계산되는지 살펴보고, 여기서 Bias-Variance Decomposition을 유도해보자.
$$\begin{align*}Err(x_0) &= E\big[y-\widehat{F}(x) | x=x_0 \big]^2\\&=E\big[(F^*(x_0)+\epsilon)-\widehat{F}(x_0) \big]^2\;\;\;\;\;(y = F^*(x)+\epsilon)\\&=E\big[F^*(x_0)-\widehat{F}(x_0)+\epsilon\big]^2\end{align*}$$
제곱항을 풀기 위해서 $F^*(x_0)-\widehat{F}(x_0)$부분을 A, $\epsilon$부분을 B라고 놓고 제곱항을 풀어보자.
$$E[A + B]^2 = E[A]^2 + E[B]^2 + 2E[AB]$$
이때 A항과 B항은 independent하기 때문에 $2E[A]E[B]$로 분해할 수 있다.
E[B]부분을 살펴보면, $E[\epsilon] = 0$임으로 (\epsilon은 평균이 0인 정규분포를 따른다) $2E[AB]$ 항이 사라진다.
$F^*(x_0)$는 상수임으로 그대로 E가 벗겨지고, $E\big[\widehat{F}_D(x)\big]=\overline{F}(x)$이다. 두 값은 같음으로, $E[A] = 0$이 되어, $2E[A]E[B]$ 항이 사라진다.
$$Err(x_0) = E\big[F^*(x_0)-\widehat{F}(x_0)\big]^2+E\big[\epsilon\big]^2$$
$\epsilon$은 평균이 0, 분산이 $\sigma^2$인 정규분포를 따름으로, $\sigma^2 = E\big[\epsilon\big]^2$이다.
$$Err(x_0) = E\big[F^*(x_0)-\widehat{F}(x_0)\big]^2+\sigma^2$$
위 식에 $\overline{F}(x_0)-\overline{F}(x_0)$항을 추가해도 문제가 없다.
$$Err(x_0) = E\big[F^*(x_0)-\overline{F}(x_0)+\overline{F}(x_0)-\widehat{F}(x_0)\big]^2+\sigma^2$$
다시 제곱항을 풀어보자. $F^*(x_0)-\overline{F}(x_0)$를 A, $\overline{F}(x_0)-\widehat{F}(x_0)$를 B로 놓고 제곱항을 풀면,
$$E[AB] = E\big[\big(F^*(x_0)-\overline{F}(x_0))(\overline{F}(x_0)-\widehat{F}(x_0)\big)\big]$$
$F^*(x_0)$와 $\overline{F}(x_0)$는 상수항이다. 따라서 $A\times E(B)$로 밖으로 나올 수 있다.
$$A\times E[B] = \bigg(F^*(x_0)-\overline{F}(x_0)\bigg)\bigg(\overline{F}(x_0) - E\big[\widehat{F}(x_0)\big]\bigg)$$
$E\big[\widehat{F}(x_0)\big] = \overline{F}(x_0)$으로 $E[AB]$항이 사라진다.
정리하면,
$$Err(x_0) = E\big[F^*(x_0)-\overline{F}(x_0)\big]^2+ E\big[\overline{F}(x_0)-\widehat{F}(x_0)\big]^2+\sigma^2$$
이번에도 $F^*(x_0)-\overline{F}(x_0)$이 상수항임으로 E가 벗겨진다.
$$Err(x_0) = \big[F^*(x_0)-\overline{F}(x_0)\big]^2+ E\big[\overline{F}(x_0)-\widehat{F}(x_0)\big]^2+\sigma^2$$
여기서 $Bias^2\big(\widehat{F}(x_0)\big) = \big[F^*(x_0)-\overline{F}(x_0)\big]^2$ 이고, $Var\big(\widehat{F}(x_0)\big) = E\big[\overline{F}(x_0)-\widehat{F}(x_0)\big]^2$이다. 정리해보자.
$$\begin{align*}Err(x_0) &= E\big[y-\widehat{F}(x) | x=x_0 \big]^2\\&=\cdots\\&= \big[F^*(x_0)-\overline{F}(x_0)\big]^2+ E\big[\overline{F}(x_0)-\widehat{F}(x_0)\big]^2+\sigma^2\\&= Bias^2\big(\widehat{F}(x_0)\big) + Var\big(\widehat{F}(x_0)\big) + \sigma^2\end{align*}$$
$Bias^2$와 $Var$이 어떤 의미인지 알아보자.
- $Bias^2$ : the amount by witch the average estimator differs from the truth.
$Bias^2$는 noise가 다른 여러 Dataset을 사용하여 반복적으로 모델링을 하였을 때, 그 모델의 평균적인 결과가 정답과 얼마나 차이나는지를 나타낸다.
$Bias^2$가 작다면 평균적으로 정답을 잘 맞출 것이다. 반면 $Bias^2$가 크다면, 정답을 잘 맞추지 못한다는 뜻이다. High bias는 poor match 라고 표현한다.
- $Variance$ : spread of the individual estimation around their mean.
$Var$은 각각의 모델들이 평균과 얼마나 다른지 그 분산을 나타낸다. 다시말해 모델들의 결과가 얼마나 넓게 퍼져있는지 아니면 잘 모여있는지를 나타낸다. $Var$이 작다면, noise가 변하더라도 결과가 크게 영향을 받지 않을 것이다. 하지만 $Var$이 크다면 noise의 변화에 크게 영향을 받아, 결과가 많이 바뀔 것이다. High variance는 week match 라고 표현한다.
- $\sigma^2$ : irreducible error which present in the original data.
$\sigma^2$는 제거할 수 없는, 자연 발생하는 noise를 나타낸다.
$Bias^2$와 $Variance$는 서로 독립적이지 않다. 그림을 통해 각 값의 의미를 살펴보자.
파란색 원으로 그려진 영역이 $\epsilon$이라는 Error를 가지는 Original data의 영역이다. 그리고 노란색 원으로 그려진 영역이 $Var$만큼 분포하는 예측 모델의 결과 영역이다. Model Bias는 $Bias^2$만큼 정답으로부터 Average가 떨어진 오차를 나타낸다. $Bias^2$와 $Variance$가 작을수록 추측하고자 하는 정답 함수에 가까워진다.
다른 예시를 보자.
주황색 원이 우리가 찾고자 하는 정답 $F^*(x)$이다. 그리고 파란색 x 표시들이 예측한 모델의 결과값이다. 알고리즘이 $Bias$와 $Variance$에 따라 어떻게 다른건지 알아보자.
- $Bias$ : High, $Variance$ : High
$Bias$도 높고 $Variance$도 높기 때문에 예측값들의 평균이 정답에서 떨어져있고, 넓게 퍼져서 분포하고 있다. 이 경우, 가장 안 좋은 성능의(잘 쓰지 않는) 모델일 것이다.
- $Bias$ : Low, $Variance$ : High
$Bias$는 낮음으로, 예측값들의 평균이 정답과 가깝다. 하지만 $Variance$가 높기 때문에 넓게 퍼져서 분포하고 있다. 이러한 대표적인 모델들은 Decision Tree, ANN, k가 작은 k-NN, 복잡한 RBF Kernel을 사용하는 등 Complexity가 높은 모델들이다.
- $Bias$ : High, $Variance$ : Low
$Variance$가 작기 때문에 개별 추정값들의 편차가 작게 좁게 모여서 분포하고 있다. 하지만 $Bias$는 높음으로, 예측값들의 평균이 정답에서 멀리 떨어져 있다. 이러한 대표적인 모델들은 Logistic regression, LDA, k가 큰 k-NN 등 Complexity가 낮은 모델들이다.
- $Bias$ : Low, $Variance$ : Low
$Bias$는 낮음으로, 예측값들의 평균이 정답과 가깝다. 동시에 $Variance$도 작기 때문에 개별 추정값들의 편차가 작게 좁게 모여서 분포하고 있다. 가장 좋은 성능의 모델일 것이다. 하지만 현실적으로 이런 모델을 만드는 것이 어렵다.
Ensemble
현실의 모델들은 두 값이 모두 낮기 어렵다. 앙상블 기법을 사용하여 위의 $Bias$만 높은 경우와 $Variance$만 높은 경우를 개선하려 한다. 앙상블 기법은 크게 두 계열로 분류된다.
- Bagging 계열
$Variance$가 작지만 $Bias$가 높은 경우, Complexity가 높은 모델에 $Variance$를 줄이기 위하여 사용한다.
- Boosting 계열
$Bias$가 작지만 $Variance$가 높은 경우, Complexity가 낮은 모델에 $Bias$를 줄이기 위하여 사용한다.
무조건 저 경우에만 사용하는 것은 아니다. 하지만 일반적으로 가장 좋은 효과를 얻기 위헤 위와 같이 조합을 한다.
Purpose of Ensemble
앙상블의 목적은 여러개의 모델을 만들어 Error를 줄이는 것이다. 위에서 보았듯이 줄이려는 변인에 따라 Bagging 계열과 Boosting계열로 나뉜다.
앙상블에 있어서 고려해야 하는 중요한 질문들이 있다.
- Q1 : How to generate individual components of the ensemble systems(base classifier) to achieve sufficient degree of diversity?
"개별적인 Component들이 어떻게 해야 충분한 다양성을 가질 것인가?" 다양성이 없게, 완전히 동일한 model을 여러개 만들어서 합치는 경우를 생각해보자. 당연하게도 이는 한개의 모델을 여러번 돌린 것과 차이가 없다.
- Q2 : How to combine the outputs of individual classifiers?
"개별적인 모델들을 어떻게 합칠 것인가?" 아무리 좋은 모델들을 합치더라도 이상한 방법으로 합친다면 오히려 성능이 나빠질 것이다. 적절한 방법을 사용하여 합치는 것이 중요하다.
앙상블 기법을 수행할 때 합쳐지는 base classifier들이 가져야 하는 두가지 조건이 있다.
- 모델들의 다양성을 확보해야 한다. (위의 Q1에서 말하는 것과 같다)
- 각각의 base model의 성능이 어느정도 좋아야 한다.
생각해보면 당연한 조건들이다. 모델이 다양하지 않다면, 앙상블 기법을 사용하는 의미가 없다. 그리고 base model의 성능이 좋지 않다면, 성능이 좋지 않은 모델들을 아무리 많이 Combine 해도 유의미한 결과를 얻지 못할 것이다.
Ensemble Diversity
계속 강조했던 Diversity는 implicit diversity와 explicit diversity로 나뉜다.
- Implicit diversity : Provide different random subset of the training data to each learner.
Implicit diversity는 각 모델마다 Dataset을 다르게 제공하여, 이를 통해 학습되는 결과가 다를 것이라 기대하는 것이다. 예시로 Bagging 계열, Random Subspaces, Rotation Forest, Random Forest 등 이 있다.
Implicit diversity를 고려하는 경우, independent하게 dataset의 instance를 선택한다.
- Explicit diversity : Use some measurement ensuring it is substantially different from the other members.
Explicit diversity를 고려하는 경우, dependent하게 다른 model의 guide를 받아 dataset의 instance를 선택한다.
이 경우 각각의 dataset을 만드는 과정에서 이전 Model의 학습이 완료될 때 까지 기다려야 한다. 이전 Model로 부터 측정 지표가 Dataset Manipulator에 전달되고 순차적으로 dataset 생성과 학습이 진행된다.
그렇다면 순차적으로 수행하는 Model Guide 방법이 병렬적으로 수행하는 Independent 방법보다 느릴까? 그렇지 않다.
Independent 방법을 사용할 모델들은 주로 Complexity가 높은 모델들이다. 반면 Model Guide 방법을 사용할 모델들은 주로 Complexity가 낮은 모델들이다. 때문에 Independent한 과정이 병렬적으로 수행되더라도 하나의 모델 학습 시간이 Model Guide 전체 모델 학습 시간보다 길다.
Why Ensemble?
앙상블 방법을 사용하는 것이 왜 더 좋은지 수학적으로 알아보자.
추정하고자 하는 True function을 $f$ 라고 할 때, 각 model의 추정 값 $y_m$은 $f$에 error를 더한 값이다.
$$y_m(x) = f(x) + \epsilon_m (x)$$
그리고 Error의 기대값 (Expected error)는 아래와 같다.
$$\mathbb{E}_x \big[ \{y_m(x) - f(x)\}^2 \big] = \mathbb{E}_x \big[ \epsilon_m(x)^2 \big] $$
위 정의를 기반으로 M개의 model들의 Average Error를 구해보자.
$$E_{Avg} = \frac{1}{M} \sum_{m=1}^M \mathbb{E}_x \big[ \epsilon_m(x)^2 \big] $$
그렇다면 앙상블 방법을 사용한 경우, Error는 어떻게 될까?
$$y_{Ensemble} = \frac{1}{M} \sum_{m=1}^M y_m(x) $$
(앙상블의 Combine 방법으로, 개별 모형 출력값의 평균을 사용한다고 가정하자)
$$\begin{align*}E_{Ensemble} &= \mathbb{E}_x \bigg[ \big\{ \frac{1}{M} \sum_{m=1}^M y_m(x) - f(x) \big\}^2 \bigg] \\&= \mathbb{E}_x \bigg[ \big\{ \frac{1}{M} \sum_{m=1}^M y_m(x) - \frac{1}{M}\times M f(x) \big\}^2 \bigg]\\ &= \mathbb{E}_x \bigg[ \big\{ \frac{1}{M} \sum_{m=1}^M (y_m(x) - f(x)) \big\}^2 \bigg]\\ &=\mathbb{E}_x \bigg[ \big\{ \frac{1}{M} \sum_{m=1}^M \epsilon_m(x) \big\}^2 \bigg]\end{align*}$$
$E_{Avg}$와 $E_{Ensemble}$을 비교하기 위해서 Error들의 평균은 0 (Zero mean)이고 서로 상관관계는 없다(Uncorrelated)라고 가정하자.
$$\mathbb{E}_x [\epsilon_m (x)] = 0,\;\;\;\;\mathbb{E}_x [\epsilon_m (x)\epsilon_l (x)] = 0\;\;(m\neq l)$$
그렇다면, 아래의 상관관계가 유도된다.
$$\begin{align*} E_{Ensemble} &= \mathbb{E}_x \bigg[ \big\{ \frac{1}{M} \sum_{m=1}^M \epsilon_m(x) \big\}^2 \bigg]\\&=\frac{1}{M^2}\mathbb{E}_x \bigg[ \big\{ \sum_{m=1}^M \epsilon_m(x) \big\}^2 \bigg]\\&=\frac{1}{M^2}\times M\times \mathbb{E}_x \big[ \epsilon_m(x)^2 \big] \;\;\;\;\;\; \bigg(\mathbb{E}_x [\epsilon_m (x)\epsilon_l (x)] = 0\bigg)\\&=\frac{1}{M}E_{Avg}\end{align*} $$
위에서 가정한 상황이라면, 앙상블을 사용한 경우, Error가 $\frac{1}{M}$으로 줄어드는 엄청난 성능 개선이 이루어진다. 하지만 현실적으로 Error의 평균이 0이지도 않고, Uncorrelated 하지 않다.
현실 상황에서 Error들이 Correlated이라 하더라도, Cauchy-Schwarz 부등식을 사용해서 상관관계를 찾을 수 있다.
$$(a_1x_1+a_2x_2+\cdots+a_kx_k)^2 \leq (a_1^2 +a_2^2+\cdots+a_k^2)(x_1^2+x_2^2+\cdots+x_k^2)$$
$$\bigg(\sum_i^ka_ix_i \bigg)^2 \leq \bigg(\sum_i^ka_i \bigg)\bigg(\sum_i^kx_i \bigg)$$
$$(Cauchy-Schwarz\;\;inequality)$$
$$\big\{ \sum_{m=1}^M \epsilon_m(x) \big\}^2=\big\{ \sum_{m=1}^M 1\times \epsilon_m(x) \big\}^2\leq \sum_{m=1}^M 1^2 \times \sum_{m=1}^M \epsilon_m(x)^2 = M\,\sum_{m=1}^M \epsilon_m(x)^2$$
$$\big\{ \frac{1}{M} \,\sum_{m=1}^M \epsilon_m(x) \big\}^2\leq \frac{1}{M} \sum_{m=1}^M \epsilon_m(x)^2$$
$$E_{Ensemble} \leq E_{Avg}$$
결론적으로 Error들이 독립적이지 않은 현실에서도, 앙상블 방법이 평균보다 더 좋고, 적어도 더 나쁘지는 않다. 또한 실증적으로 실험을 통해 앙상블 방법을 사용한 경우가 가장 좋은 성능의 단일 모델보다 대부분 더 좋은 성능을 보인다.
※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 정리하고, 공부한 내용을 추가하여 작성되었습니다.







댓글
댓글 쓰기