Dimensionality Reduction (요약)

-
 1. Feature extraction / Dimensionality reduction
  • Given data points in $d$ dimensions
  • Convert them to data points in $k(<d)$  dimensions
  • With minimal loss of information

2. Principal Component Analysis (PCA)
  • Find k-dim projection that best preserves variance
  • Process
    1. compute mean vector $\mu$ and covariance matrix $\Sigma$ of original data $$\Sigma = \frac{1}{N}\sum_{i=1}^N (x_i - \mu)(x_i-\mu)^T $$
    2. Compute eigenvectors and eigenvalues of $\Sigma$ $$\Sigma v = \lambda v $$
    3. Select largest $k$ eigenvalues (also eigenvectors)
    4. Project points onto subspace spanned by them $$y = A(x - \mu)$$
  • Eigenvector with largest eigenvalue captures the most variation among data $X$
  • We can compress the data by using the top few eigenvectors (principal components)
  • Feature vector $y_k$'s are uncorrelated (orthogonal)

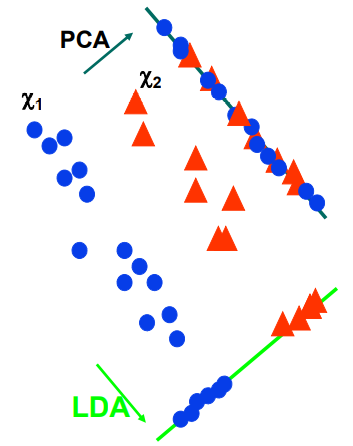
3. Linear Discriminant Analysis (LDA)
  • PCA vs. LDA
    • PCA does not consider "class" information
    • LDA consider "class" information
    • PCA maximizes projected total scatter
    • LDA maximizes ratio of projected between-class to projected within-class scatter
  • Within-class scatter (want to minimize) $$\Sigma_w = \sum_{j=1}^c \frac{1}{N_c}\sum_{i=1}^{N_c} (x_i -\mu_c)(x_i -\mu_c)^T $$
  • Between-class scatter (want to maximize) $$\Sigma_b = \frac{1}{c}\sum_{i=1}^c (\mu_i -\mu)(\mu_i -\mu)^T $$
  • Compute eigenvectors and eigenvalues $$\frac{\Sigma_b}{\Sigma_c}v = \lambda v $$















댓글

댓글 쓰기

이 블로그의 인기 게시물

One-Class SVM & SVDD

-
이미지
03_6 : Anomaly Detection : Auto-Encoder, 1-SVM, SVDD MoG와 같은 밀도기반 방법론들은 특정 객체가 정상범주에 속할 확률을 구했다. 반면 Support vector 기반 방법론들은 normal과 abnormal을 구분하는 분류경계면을 찾는다. 이번 글에서는 Support vector 기반의 Anomaly detection 방법 중 one-class SVM과 SVDD를 알아보자. One-class Support Vector Machine (1-SVM, OCSVM) 1-SVM의 목표는 Data를 feature space로 mapping 한 뒤, 분류경계면을 통해 mapping된 Data 중 normal data들이 원점으로부터 최대한 멀어지게 만드는 것이다. 위 그림에서 파란색 분류경계면이 (+1) normal data들을 구분하는 것을 확인할 수 있다. 이 목표를 수식화 한 Optimization problem부터 살펴보자. Optimization Problem $$\min_{\textbf{w}}\;\;\;\frac{1}{2}||\textbf{w}||^2 + \frac{1}{\nu l} \sum_{i=1}^l \xi_i - \rho$$ $$s.t.\;\;\;\textbf{w}\cdot \Phi (x_i) \geq \rho - \xi_i\;\;\;\;(i=1,2,\cdots,l),\;\;\xi_i\geq 0$$ $\frac{1}{2}||\textbf{w}||^2$ term은 SVR과 같이 $x$의 변화에 따른 변동이 크지 않도록 Regularization을 하는 term이다. $\rho$는 위 그림에서 주황 직선을 나타내는데, 원점과 분류경계면 Hyperplane과의 거리를 나타낸다. 이 값을 뺌으로써 최소화 문제를 만족하는 최적해일때 $\rho$가 최대가 되도록 한다. (원점에서 Hyperplane이 최대한 멀어지게 만든다) $\frac{1}{\nu l} \sum_{i=1}^l \xi_i$ term은 제약식에 따라 Hyp...
자세한 내용 보기

Support Vector Regression (SVR)

-
이미지
02_4 : Kernel based learning : Support Vector Regression (SVR) 앞에서 공부했던 SVM은 binary classification을 하기 위한 방법이었다. 이번 글에서 알아볼 SVR은 함수를 추정하여 연속적인 수치변수를 예측하는 회귀 방법이다.  SVR을 알아보기에 앞서 우리가 하려는 함수추정의 목적을 살펴보자. Fitting function 함수를 추정하고 싶을 때 우리의 목적은 크게 2가지로 나뉜다. Minimize an error measure (Loss function) 한마디로 error를 최소화 하여야 한다. (잘 맞춰야 한다) Function to be simple 같은 성능이라면, 함수는 최대한 단순해야 한다. 함수가 단순하다는 뜻은 아래의 조건들을 의미한다. Fewest basis functions Simplest basis functions Flatness is desirable Support Vector Regression (SVR) 위에서 살펴보았던 Loss function과 Flatness를 반영하도록 목적함수를 만들 것이다. SVR에도 여러 종류가 있는데, 우선 $\varepsilon$-SVR에 대하여 알아보자. 현실의 Data들은 어쩔 수 없이 발생하는 noise가 존재한다. 아래 식에서 noise는 $\varepsilon$이다. $$y = f(x)+\varepsilon$$ $\varepsilon$-SVR에서 핵심 아이디어는 $\varepsilon$ 보다 작은 noise에 대해서는 Loss를 주지 말자는 것이다.  왼쪽 그림에서 색이 칠해진 영역을 Epsilon-tube 라고 하는데, 이 영역안에 있는 객체들에게는 Loss를 부여하지 않는다. 이를 위한 Loss function은 오른쪽에 표현된다. 이 Loss function은 hinge를 닮았다고 해서, Hinge Loss 라고 불린다. 차이가 $\varepsilon$ 보다 작은 경우 loss는 0이고, $\vareps...
자세한 내용 보기

Self-Training & Co-Training

-
이미지
 05_2 : Semi-Supervised Learning : Self-Training and Co-Training 우선 가장 기본적인 준지도학습 방법 Self-Training에 대하여 알아보자.  Self-Training 우리에게 주어진 정보는 Labeled data $(\mathbf{X}_l,y_l)$과 Unlabeled data $\mathbf{X}_u$이다. Self-training과정은 다음과 같이 진행된다.  1. 우선 주어진 Labeled data $(\mathbf{X}_l,y_l)$를 사용하여 예측함수 $f$를 학습시킨다. $$y_l = f(x_l)$$ 2. 학습이 완료되면, 예측함수 $f$를 사용해 Unlabeled data $\mathbf{X}_u$의 예측값 $\hat{y}_u$를 구한다. $$\hat{y}_u = f(x_u)$$ $$\Downarrow$$ 3. 이제 기존의 Labeled data와 예측함수에 의해 labeling이 된 Unlabeled data를 합치고, 이 data를 사용해 예측함수 $g$를 학습한다. 이때 어떻게 Unlabeled data를 합치는지에 따라서 많은 variation이 있다. 대표적으로 Add all $(x_u,\hat{y}_u)$ to labeled data Add a few most confident $(x_u,\hat{y}_u)$ to labeled data Add all $(x_u,\hat{y}_u)$ to labeled data, weight each by confidence. 모든 Unlabeled data를 합치는 방법, 몇몇개의 가장 예측 confidence가 높은 data만을 합치는 방법, 모든 data를 합치치만 예측 confidence에 따라서 weight를 지정하는 방법 등이 있다. 4. 위와 같은 과정을 Unlabeled data가 없어지거나, 수렴할 때 까지 반복한다. Propagating 1-Nearest Neighbor 다른 예시로 Propagating ...
자세한 내용 보기