Gaussian Density Estimation

03_2 : Anomaly Detection : (Mixture of) Gaussian Density Estimation

Density-based Novelty Detection

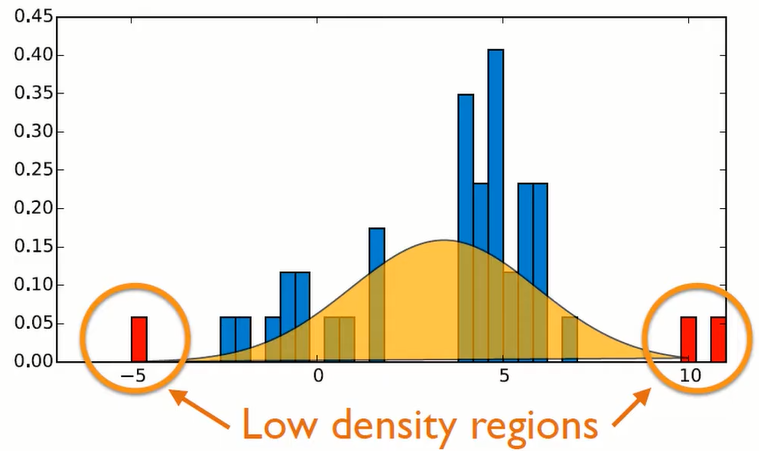
밀도 기반의 이상치 탐지 방법의 목적은 주어진 data를 기반으로 normal data의 분포를 추정하고, 추정한 분포를 사용하여 새로운 data가 주어졌을 때 발생할 확률을 구할 수 있다. 만약 발생 확률이 높다면 Normal data라고 판별하고, 낮다면 Abnormal data라고 판별한다.

만약 3이 input data로 주어진다면 추정한 가우시안 분포에 높은 확률 분포임으로 normal data라고 판별할 것이다. 하지만 -5가 input data로 주어진다면 가우시안 분포에서 낮은 확률 분포임으로 abnormal data라고 판별할 것이다.

여기서 주의할 점은 주어진 data가 가우시안 분포인지 아닌지를 모른다는 점이다. 때문에 이 방법을 사용하기 전에 적합한 data인지 판단하고 사용하어야 한다.

Density-based Novelty(Abnormal) Detection 방법은 여러 종류가 있다. 먼저 전체 data가 하나의 가우시안 분포로부터 생성되었다는 가정하에 하나의 가우시안 분포를 추정하는 Gaussian Density Estimation이 있다. 즉 전체 Modal의 수가 1개이다.

두번째는 여러개의 가우시안 분포의 합성으로 이루어진 분포로부터 생성되었다는 가정하에 여러개의 가우시안 분포를 추정하는 Mixture of Gaussian Density Estimation이 있다. 이 경우 Modal의 수가 $1\leq (Number\;of\;modals)\leq (Number\;of\;instances)$를 만족한다.

세번째는 두번째 경우가 극한으로 표현한 경우이다. 모든 각 객체가 각 가우시안 분포의 중심이라 가정하고 이로부터 객체의 수 만큼의 가우시안 분포를 추정하는 방법이다.

이번에 알아볼 것은 Gaussian Density Estimation과 Mixture of Gaussian Density Estimation이다. 이 글에서는 Gaussian Density Estimation을 알아보자.

---

Gaussian Density Estimation

우리의 가정은 주어진 Data가 하나의 가우시안 분포로 부터 생성되었다는 것이다. 입력변수가 다차원인 경우의 가우시안 분포는 다변량 가우시안 분포라 하며 우리가 흔히 알고있는 가우시안 분포의 식과는 좀 다르다. (가우시안 분포를 잘 모르겠다면 이 블로그를 참고해보자. 가우시안 분포)

$$p({x}) = \frac{1}{(2\pi )^{d/2}|\Sigma|^{1/2}}\exp\bigg[-\frac{1}{2}({x}-{\mu})^T\Sigma^{-1}({x}-{\mu})\bigg]$$

$$\mu = \frac{1}{n}\sum_{x_i\in X^+} {x}_i\;\;\;\;\;\;(mean\;vector)$$

$$\Sigma = \frac{1}{n}\sum_{x_i\in X^+}({x}_i-{\mu})({x}_i-{\mu})^T\;\;\;\;\;\;(covariance\;matrix)$$

위 식에서 $x_i\in X^+$가 의미하는 것은 normal data집합 $X^+$의 원소 $x_i$를 사용하겠다는 뜻이다. 결론적으로 normal data $X^+$가 주어졌을 때 우리는 미지수 ${\mu}$와 $\Sigma$를 계산해야 한다. 그리고 그 계산을 통해 다변량 가우시안 분포를 구할 수 있다.

Gaussian Density Estimation의 장점은 2가지가 있다.

첫번째로 Data의 변수 범위(단위)에 robust 하다. (Insensitive to scaling of the data) 대다수의 모델들은 변수의 범위가 다를때 정규화를 통해 범위를 조절해 주어야 한다. 하지만 Gaussian Density Estimation은 Covariance matrix의 역행렬 $\Sigma^{-1}$을 사용하기 때문에 변수의 범위가 동작에 영향을 미치지 않는다. (쉽게 말해, 어차피 모두 0~1사이의 분산값으로 계산하여 사용하기 때문이다)

두번째로 Optimal 한 threshold를 분석적으로 계산할 수 있다. (Possible to compute analytically the optimal threshold) Model을 정의할 때 분포를 통해 추정된 가우시안 분포가 몇 %의 오류를 가질지 정하고, 이 값에 따라 cut-off를 조절하여 가우시안 분포의 rejection region을 지정할 수 있다.

이외에도 가우시안 함수를 알고있기 때문에 함수의 미분이나 특성을 이용한 다양한 분석이 가능하다.

---

Maximum Likelihood Estimation

그렇다면 어떠한 가우시안 분포가 해당 data를 얼마나 잘 반영하고 있는지 어떻게 판단할까? 일반적으로 Likelihood(우도)를 사용하여 이를 판단한다. 어떤 1차원 data에 대하여 가우시안 분포가 주어졌다면, 가우시안 분포 식은 다음과 같을 것이다.

$$p({x}) = \frac{1}{(2\pi \sigma^2)^{1/2}}\exp\bigg[-\frac{1}{2\sigma^2}({x}-{\mu})^2\bigg]$$

해당 가우시안 분포에서 하나하나의 변수 $x_i$가 선택될 확률은 $p(x_i) = p(x_i|\mu,\sigma^2)$이다. ($\mu$와 $\sigma$는 생략하기도 한다) 그리고 어떤 가우시안 분포가 data를 얼마나 잘 반영하는지 나타내는 likelihood는 다음과 같다. 

(이때 independent identically distributed(iid) : "동일한 확률분포에서 각각의 객체가 독립적으로 생성됨"을 가정해야 한다)

$$L = \prod_{i=1}^Np(x_i|\mu,\sigma^2) = \prod_{i=1}^N\frac{1}{\sqrt{2\pi  }\sigma }\exp\bigg[-\frac{({x}_i-{\mu})^2}{2\sigma^2}\bigg]$$

이 Likelihood를 최대화 하는 가우시안 함수가 data를 가장 잘 반영하는 함수일 것이다. $\log$ 함수는 단조증가함수이기 때문에 $L$의 최대화는 $\log L$의 최대화와 동치이다. 따라서 곱셈을 덧셈으로 바꿀 수 있다.

$$\log L = -\frac{1}{2}\sum_{i=1}^N \frac{({x}_i-{\mu})^2}{\sigma^2} - \frac{N}{2}\log(2\pi \sigma^2)$$

이제 이 식에서 최대값을 가지는 경우 최적해 조건에 따라 두 미지수 $\mu$와 $\sigma$로 미분한 값이 0이어야 한다. 계산을 쉽게 하기 위해 $\frac{1}{\sigma^2}=\gamma$로 치환하자.

$$\log L = -\frac{1}{2}\sum_{i=1}^N \gamma ({x}_i-{\mu})^2 - \frac{N}{2}\log(2\pi) + \frac{N}{2}\log(\gamma)$$

이제 두 미지수 $\mu$와 $\sigma$로 미분해보자.

$$\frac{\partial \log L}{\partial \mu} = \gamma\sum_{i=1}^N ({x}_i-{\mu}) = 0\;\;\Rightarrow\;\;\mu = \frac{1}{N}\sum_{i=1}^N x_i$$

$$\frac{\partial \log L}{\partial \gamma} = -\frac{1}{2}\sum_{i=1}^N ({x}_i-{\mu})^2 + \frac{N}{2\gamma} = 0\;\;\Rightarrow\;\;\frac{1}{\gamma} = \sigma^2 = \frac{1}{N}\sum_{i=1}^N ({x}_i-{\mu})^2$$

놀랍게도 최적해를 가지는 조건을 확인해 보면, $\mu$는 $x_i$들의 평균이고, $\sigma^2$은 $x_i$들의 분산임을 확인할 수 있다.

다시말해 어떤 정규분포가 데이터를 가장 잘 표현하려면 정규분포의 평균과 분산에 대응하는 값이 해당 데이터의 평균과 분산이어야 한다는 뜻이다.

이것을 일반화 하여 다차원 데이터를 표현하는 다변량 가우시안 분포에 대하여 Likelihood가 최적해를 가지는 경우의 조건을 구해보자.

$$\mu = \frac{1}{N}\sum_{i = 1}^N {x}_i$$

$$\Sigma = \frac{1}{N}\sum_{i = 1}^N ({x}_i-{\mu})({x}_i-{\mu})^T$$

계산을 생략하고 결과를 살펴보면, 위와 같이 가우시안 함수의 평균 vector $\mu$는 Data의 평균 vector가 되고, 가우시안 함수의 공분산행렬 $\Sigma$는 Data의 공분산 행렬이 된다.

이와 같이 Gaussian Density Estimation 방법은 Data의 평균 vector와 공분산행렬만 계산하면 되기 때문에 수행속도가 굉장히 빠르다.

---

Covariance matrix

어떤 형식의 공분산행렬을 사용하는지에 따라서 가우시안 함수의 모양이 달라진다. 

• Spherical

$$\sigma^2 = \frac{1}{d}\sum_{i=1}^d\sigma_{i}^2\;\;\Sigma = \sigma^2\begin{equation*} \begin{bmatrix} 1&\cdots & 0\\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{bmatrix}\end{equation*}$$

모든 변수들은 독립이고 모든 변수들이 동일한 분산을 가졌다고 가정하여, 모든 분산을 평균한 값을 단위행렬에 곱한 뒤 이를 공분산 행렬로 사용하는 경우이다.

이 경우 행렬의 대각성분 외에는 모두 0이고, 대각성분이 모두 동일한 값을 가지기 때문에 정규분포 모양의 함수가 그려진다. 위의 그림을 보면 함수의 등고선이 영점을 중심으로 원형으로 그려지는 것을 확인할 수 있다.

• Diagonal

$$\Sigma = \begin{equation*} \begin{bmatrix} \sigma_1^2&\cdots & 0\\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_d^2 \end{bmatrix}\end{equation*}$$

모든 변수들은 독립이지만, 각 대각성분의 분산은 다를 수 있다고 가정을 좀더 완화한 경우이다.

이 경우 행렬의 대각성분 외에는 모두 0이기 때문에 축의 장축과 단축을 기준으로 평행한 타원이 그려진다.

• Full

$$\Sigma = \begin{equation*} \begin{bmatrix} \sigma_{11}^2&\cdots & \sigma_{1d}^2\\ \vdots & \ddots & \vdots \\ \sigma_{d1}^2& \cdots & \sigma_{dd}^2 \end{bmatrix}\end{equation*}$$

모든 변수들이 독립이 아니고, 모든 분산이 다를 수 있다고 가정을 완전히 완화한 경우이다.

이 경우 축이 변환된 타원이 그려진다. 

우리가 위에서 표현했던 최적의 공분산 행렬은 일반적으로 Full 형태를 띌 것이다. 공분산 행렬의 역행렬이 존재하고, 계산이 가능하다면 Full형태를 사용하는 것이 가장 좋을 것이다. 하지만 변수가 매우 많은 현실의 data를 계산할 때, 공분산 행렬이 singular matrix가 되어서 역행렬이 없는 경우가 많다. 때문에 일반적으로 가정이 조금 완화된 Diagonal형태의 공분산 행렬을 많이 사용한다.

※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 정리하고, 공부한 내용을 추가하여 작성되었습니다.