Support Vector Machine (SVM) - Linear & Hard margin
02_2 : Kernel based learning : Support Vector Machine (SVM) - Linear & Hard margin
Discriminant Function in classification
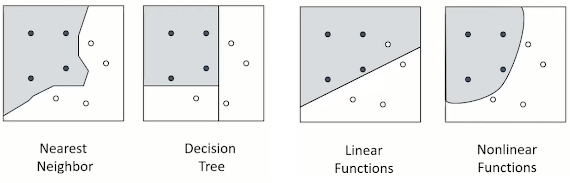
Binary Classification 문제가 주어졌을때 classification을 수행하는 방법은 크게 4가지가 있다.
Binary Classification Problem
우선은 우리가 해결할 Binary classification 문제를 정의해보자.
- Training data
Sample drawn i.i.d from set $X\in\mathbb{R}^d$ according to some distribution D
$$S=\{(x_1,\,y_1),\,(x_2,\,y_2),\,\cdots ,\,(x_n,\,y_n)\} \in X \times \{-1,+1\}$$
i.i.d는 independent and identically distributed를 뜻한다. binary classification임으로 각 class를 구분하는데, 0, 1이 아니라 +1과 -1로 구분하는 이유는 SVM의 수학적 formulation을 좀더 간략히 하기 위해서이다.
- Problem
Find hypothesis $h\;:\;X\rightarrow \{-1,+1\}$ in H(classifier) with small generalization error $R_D(h)$
구조적 위험 최소화 관점에서 일반화 된 error $R_D$를 최소화 하는 분류기 H를 만드는 것이 목표이다.
또한 SVM은 linear classifier임으로 고차원 상에서 high-dimensional data를 분류하는 Hyperplane을 찾는것이 목표이다.
$g(\textbf{x})=\textbf{w}^T\textbf{x}+b$로 표현되는 linear classifier에 대해서 살펴보자.
선형 분류기는 $sign$함수에 의해 $\textbf{w} \cdot \textbf{x}+b$식의 직선 그래프를 기준으로 위쪽은 +1, 아래쪽은 -1을 반환하게 된다.
선형 분류기는 $\textbf{w} \cdot \textbf{x}+b$ 식의 미지수 $\textbf{w}$와 $b$에 따라 다양하게 만들어질 수 있다.
그렇다면 어떤 선형 분류기가 더 좋은 분류기일까?
이전 글에서 구조적 위험을 공부하였다.
$$R[f] \leq R_{emp}[f] + \sqrt{\frac{h(ln\frac{2n}{h}+1)-ln(\frac{\delta}{4})}{n}}$$
구조적 위험에 대한 식을 간략화 하면 아래와 같이 축약할 수 있다.
$$R = R_{emp} + (Capacity\;\,Term)$$
우리의 목표는 구조적 위험 $R_D[f]$을 최소화 하는 분류기 H를 찾는 것이다. 두 분류기 모두 100%의 분류 성능을 보인다. 따라서 두 분류기 모두 $R_{emp} = 0$이다. 그렇다면 $(Capacity\;\,Term)$은 어떨까?
그림을 다시 살펴보자. 분류기의 분류 경계면은 직선으로 표현되는데, 이 파란색 직선에 대하여 연한 파란색으로 색이 칠해져 있다. 이 영역은 분류 경계면으로부터 가장 가까운 양쪽 범주 객체와의 거리를 나타내고 있으며, 이 거리를 margin이라고 한다.
이유는 아래에서 이야기 하도록 하고, 먼저 결론만 이야기 하면, margin이 크면 $(Capacity\;\,Term)$이 감소하고, margin이 작다면 $(Capacity\;\,Term)$이 증가한다. 따라서 우리는 margin이 더 커서 구조적 위험이 더 작은 A를 더 좋은 분류기로 선택한다.
우리가 찾고자 하는 "구조적 위험 최소화 관점에서 일반화 된 error $R_D$를 최소화 하는 분류기 H"는 margin을 최대로 하는 분류기이다.
Artificial Neural Network가 이론적으로 비판을 받았던 부분도 이것과 관련이 있다.
Artificial Neural Network
인공신경망은 구조적 위험을 최소화에 기반하지 않고 경험적 위험 최소화 만을 고려한다. 한마디로 $R_{emp}$만을 고려하고 $(Capacity\;\,Term)$을 생각하지 않는다. 따라서 인공 신경망 모델에서는 위의 A 분류기와 B 분류기를 같은 것으로 취급한다. SVM과 같이 항상 Global optimum(A)를 찾는 것이 아니라 Local optimum(B)에 빠질 가능성이 있다.
그 이유는 자연어나 사진과 같은 고차원 데이터의 특성에 있다.
기존의 과학자들은 고차원 데이터라고 하더라도 local optimum가 존재하여 인공신경망에 문제가 발생할 것으로 생각했다. 하지만 실험적으로 고차원 데이터를 분석 해보니, 모든 방향으로 Gradient가 0인 local optimum가 거의 없다는 사실을 발견하게 되었다.
이제 다시 SVM으로 돌아가자.
Support Vector Machine : Formulation
우리가 찾고자 하는 Hyperplane은 margin을 최대화 하는 Hyperplane이다.
margin을 최대화 하는 Hyperplane은 선형 분류기 $\textbf{w} \cdot \textbf{x}+b=0$으로 표현되는데, margin을 최대로 하기 위해서 +1 class에 접하는 Hyperplane에 대하여 상수항 +1을, -1 class에 접하는 Hyperplane에 대하여 상수항 -1을 추가하여 정의한다.
이를 통해서 두 Hyperplane(점선) $\textbf{w} \cdot \textbf{x}+b=+1$과 $\textbf{w} \cdot \textbf{x}+b=-1$ 사이 중앙에 Hyperplane(실선) $\textbf{w} \cdot \textbf{x}+b=0$을 구할 수 있다.
이제 $X$와 $Y$가 주어졌을 때, $\left|\textbf{w} \cdot \textbf{x}+b\right|=1$에 가장 가까운 점이 되도록 하는 미지수 $\textbf{w}$와 $b$를 구해야 한다.
먼저 margin을 계산해보자.
그렇다면 $w^T x_0+b=0$ 이다. $w$는 경계면의 법선 vector이다.
$w^T x+b=1$ 경계면 상의 점 $x_1$은 아래와 같이 표현 가능하다.
$$x_1 = x_0 + pw$$
$w^T x+b=1$ 경계면 상에 있음으로,
$$w^T x_1+b=w^T (x_0 + pw)+b = 1$$
정리하면
$$w^T x_0 + b + p\cdot w^Tw = 1$$
$w^T x_0 + b = 0$임으로,
$$p\cdot w^Tw = 1$$
$$p = -\frac{1}{w^Tw} = -\frac{1}{||w||^2}$$
$$margin = \left|p\right| = \frac{1}{||w||^2}$$
다음과 같이 margin을 구할 수 있다.
이제 위에서 생략했던, margin을 최대화 하는것이 $(Capacity\;\,Term)$을 최소화 하는 것인지 그 이유를 알아보자.
자세한 증명은 너무 많기 때문에 생략하고, 결론부터 살펴보자.
"VC dimension은 margin에 의해서 bound 된다."
<원문>
The VC dimension of separating hyperplane with a margin $\Delta$ is bounded as follows
$$h\leq min\bigg(\bigg\lceil\frac{R^2}{\Delta^2}\bigg\rceil,\,D\bigg)+1$$
where $D$ is the dimensionality of the input space, and $R$ is the radius of the smallest sphere containing all the input vectors
$D$는 input의 차원수(dimensionality)이고, $R$은 전체 data를 감싸는 가장 작은 초구(Hypersphere)의 반지름 그리고 $\Delta$가 margin이다.
input data가 주어졌을 때 $D$와 $R$은 고정된다. 그렇다면 우리가 분류 경계면의 margin을 충분히 크게 하여, $\lceil\frac{R^2}{\Delta^2}\rceil < D$이게 된다면, VC dimension $h$는 $h \leq \lceil\frac{R^2}{\Delta^2}\rceil + 1$일 것이다.
우리가 앞서 배운 Shatter의 개념에서 VC dimension $h$는 $D+1$이었다. 하지만 margin이 충분히 크다면 VC dimension은 $D+1$보다 더 작게, 최소한 $\lceil\frac{R^2}{\Delta^2}\rceil + 1$보다 작게 만들 수 있다는 것이 이 정리의 결론이다.
따라서, margin을 최대화 하면, VC dimension을 줄일 수 있고, 구조적 위험$R$을 줄일 수 있다.
$$R[f] \leq R_{emp}[f] + \sqrt{\frac{h(ln\frac{2n}{h}+1)-ln(\frac{\delta}{4})}{n}}$$
Maximize the margin $\Rightarrow$ Minimizing the VC dimension $\Rightarrow$ Minimizing the Expected Risk
이해를 돕기위해 예시를 살펴보자.
왼쪽 예시보다 오른쪽 예시의 margin이 더 작다. margin이 더 작은 오른쪽 예시는 여러 경우에서 분류 경계면을 형성할 수 있다. 이 다양한 분류 경계면들이 local optimum일 것이다.
반면 왼쪽 예시와 같이 margin을 최대로 하게 되면, 분류경계면은 단 하나만 형성된다. 이것이 구조적 위험을 최소화 하는 global optimum일 것이다.
Support Vector Machine : Hard margin vs. Soft margin
SVM은 margin을 벗어나는 예외를 허용하는 Soft margin 방법과, 허용하지 않는 Hard margin 방법으로 구분된다. 지금까지 공부했던 내용들은 Hard margin 방법의 SVM이다.
Soft margin의 경우 Penalty term을 목적함수에 추가함으로써 margin을 벗어나는 예외를 허용한다.
그런데 만약 data가 linearly separate가 되지 않는다면 Hard margin 방법을 사용할 수 없는 것일까? 그렇지 않다. Data가 linearly non-separate인 경우 Kernel Trick 방법을 사용하여 SVM이 잘 작동하도록 만들어준다.
하지만 Hard margin을 사용하는 SVM에서 linearly non-separate data를 다루는 경우 일반적으로 성능이 그닥 좋지 않다. 때문에 Soft margin을 사용하는 SVM에 Kernel Trick까지 적용하여 linearly non-separate data를 다룬다. 정리하면 아래와 같다.
| Hard margin | Soft margin | |
| Linearly separable | Basic form (Case 1) | Introduce penalty terms (Case 2) |
| Linearly non-separable | Utilize Kernel trick | Introduce penalty terms Utilize Kernel trick (Case 3) |
Case 1부터 Case 3까지 SVM은 기본적인 형태에서 점차 확장된다. Case 1부터 차례대로 알아보자.
SVM - Case 1 : Linear case & Hard margin
지금부터 알아볼 SVM은 Linearly separable 한 data에 Hard margin을 사용하는 경우이다.
Case 1의 SVM을 최적화 문제로 나타내보자.
위에서 구한 margin에 대한 식을 살펴보자. 우리의 목표는 margin을 최대화 하는 것 임으로, 상수항을 곱해주어도 문제가 없다. 기존의 식에 2를 곱해주자. (곱해주는 이유는 나중에 미분할 때 식을 간단하게 만들기 위해서이다)
$$maximize\;\;\;(margin) = \frac{2}{||w||^2}$$
margin을 최대화 하는 문제는 margin의 역수를 최소화 하는 문제와 동치이다.
$$minimize\;\;\;(\frac{1}{margin}) = \frac{1}{2}||w||^2$$
이제 제약조건을 구해보자.
$$if\;\;y_i=+1,\;\;w^Tx_i+b \geq 1$$
$y_i$는 1임으로 양변에 곱하여도 부등호가 변하지 않는다.
$$y_i(w^Tx_i+b) \geq 1$$
이제 $y_i = -1$인 붉은색 point들을 살펴보자. 붉은색 point들은 항상 $w\cdot x +b=-1$ 직선의 아래에 존재해야 한다.
$$if\;\;y_i=-1,\;\;w^Tx_i+b \leq -1$$
$y_i$는 -1임으로 양변에 곱하면 부등호가 변한다.
$$y_i(w^Tx_i+b) \geq 1$$
놀랍게도 $y_i$가 1인 경우와 -1인 경우 모두 제약식이 일치한다. 덕분에 제약식을 모든 $i$에 대한 하나의 식으로 표현할 수 있다.
- Objective function
$$min\;\;\frac{1}{2}||\textbf{w}||^2$$
- Constraints
$$ s.t.\;\;y_i(\textbf{w}^T\textbf{x}_i+b)\geq 1, \;\;\;\;\forall i$$
그러면 위의 제약이 있는 최적화 문제 Primal problem ($L_p$)를 Lagrangian Multiplier 방법을 사용하여 제약이 없는 Dual problem ($L_d$)로 바꾸어 보자.
위의 Primal 최적화 문제를 라그랑주 승수법을 사용하여 표현해보자.
$N$개의 제약식 $y_i(\textbf{w}^T\textbf{x}_i+b)\geq 1$에 라그랑주 승수를 곱하여 제약을 제거한다.
- Lagrangian problem
$$min\;\;L_P(\textbf{w},b,\alpha_i)=\frac{1}{2}||\textbf{w}||^2-\sum_{i=1}^N\alpha_i(y_i(\textbf{w}^T\textbf{x}_i+b)-1)\;\;\;\;s.t.\;\;\alpha_i\geq0$$
이제 이 라그랑주 문제에 KKT Condition을 만족하는 최적해를 찾을 것이다.
KKT Condition 중 Stationarity 조건에 따라 모든 변수에 대한 미분값은 0이어야 한다. 따라서 아래의 두 식을 도출할 수 있다.
$$\frac{\partial L_P}{\partial \textbf{w}} = w-\sum_{i=1}^N \alpha_iy_ix_i = 0$$
$$\therefore \textbf{w} = \sum_{i=1}^N \alpha_iy_ix_i$$
$$\frac{\partial L_P}{\partial b} = -\sum_{i=1}^N \alpha_iy_i = 0$$
$$\therefore \sum_{i=1}^N \alpha_iy_i = 0$$
KKT Condition으로부터 도출한 $\textbf{w} = \sum_{i=1}^N \alpha_iy_ix_i$을 $L_P$에 대입하여 Dual problem으로 바꾸자.
- Dual problem
$$L_P=\frac{1}{2}||\textbf{w}||^2-\sum_{i=1}^N\alpha_i(y_i(\textbf{w}^T\textbf{x}_i+b)-1)$$
$$\begin{align*}L_D &= \frac{1}{2}||\sum_{i=1}^N \alpha_iy_ix_i||^2-\sum_{i=1}^N\alpha_i(y_i((\sum_{i=1}^N \alpha_iy_ix_i)^T\textbf{x}_i+b)-1)\\&=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_ix_j - \sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_ix_j -b\sum_{i=1}^N \alpha_iy_i + \sum_{i=1}^N\alpha_i\\&=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_ix_j\;\;\;\;\;\;(\sum_{i=1}^N \alpha_iy_i = 0)\\&\;\;\;\;s.t.\;\;\sum_{i=1}^N \alpha_iy_i = 0,\;\;\;\alpha_i\geq 0\end{align*}$$
위에서 Dual에 대하여 공부했다면 Dual 함수는 Convex 함수라는 점을 알고있을 것이다. 굳이 그것을 모르더라도 위의 식을 살펴보면 $\alpha$에 대한 Convex 라는 점을 알 수 있다. $L_D$함수를 다시한번 살펴보자.
$$L_D =\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_ix_j$$
우리는 $x$와 $y$에 대해서 알고있음으로, 위 식은 $\alpha$라는 미지수에 대한 함수이다.
즉, $-\frac{1}{2}\lambda\alpha^2+\alpha$ ($\lambda$는 $x,y$로 계산된 값)꼴의 $\alpha$에 대한 Convex 함수로 볼 수 있다. 때문에 항상 극대점에 해당하는 최적해를 찾음을 보장할 수 있다.
정리해보자.
margin 최대화 문제를 margin의 역수의 최소화 문제 Primal problem으로 정의하였고, 이 문제의 해결을 위해 Dual problem으로 바꾸었다. 문제 해결을 위해 $\alpha$를 구하면 된다.
- Lagrangian problem
$$\begin{align*}min\;\;L_P(\textbf{w},b,\alpha_i)&=\frac{1}{2}||\textbf{w}||^2-\sum_{i=1}^N\alpha_i(y_i(\textbf{w}^T\textbf{x}_i+b)-1)\\&\;\;\;\;s.t.\;\;\alpha_i\geq0\end{align*}$$
- Dual problem
$$\begin{align*}max\;\;L_P(\alpha_i)&=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_ix_j\\&s.t.\;\;\sum_{i=1}^N \alpha_iy_i = 0,\;\;\;\alpha_i\geq 0\end{align*}$$
$\alpha$를 구했다면, 새로운 $x_{new}$가 주어졌을 때 어떻게 분류할까? 처음으로 돌아가 분류기의 정의를 살펴보자.
$$H = \{x\rightarrow sign(\textbf{w} \cdot \textbf{x}+b)\,:\,\;\textbf{w}\in \mathbb{R}^d\,,\;\,b\in\mathbb{R}\}$$
새로운 $x_{new}$는 위의 분류기에 의해 범주를 결정할 것이다.
$$sign(\textbf{w} \cdot \textbf{x}_{new}+b)$$
위에서 구한 $\textbf{w} = \sum_{i=1}^N \alpha_iy_ix_i$를 대입하자.
- Solution
$$f(\textbf{x}_{new}) = sign\bigg(\sum_{i=1}^N \alpha_iy_ix_i^T\textbf{x}_{new}+b\bigg)$$
새로운 $x_{new}$가 주어지면 위의 함수 $f$를 통해 범주를 구할 수 있다.
SVM - Case 1 : Linear case & Hard margin (Add.)
KKT Condition을 통해서 SVM에서 추가적으로 알 수 있는 정보들이 있다.
- Supprot vector
최적해를 가지는 경우, 라그랑주 승수법을 사용했음으로 Lagrangian multiplier와 제약식의 곱은 항상 0이어야 하고, 동시에 둘다 0이면 안된다. ($\leftarrow$ 정확히는 무조건 0이 아닌 것은 아니다. 하지만 SVM은 둘다 0인 경우가 없다는 증명이 되어있다. 이 부분은 적당히 넘어가자)
$$\alpha_i(y_i(\textbf{w}^T\textbf{x}_i+b)-1) = 0$$
$$if\;\;\;\alpha_i = 0\;\;\;\;\Rightarrow\;\;\;\;y_i(\textbf{w}^T\textbf{x}_i+b)-1\neq 0$$
$$if\;\;\;\alpha_i \neq 0\;\;\;\;\Rightarrow\;\;\;\;y_i(\textbf{w}^T\textbf{x}_i+b)-1= 0$$
이 중 $\alpha_i \neq 0$인 경우를 보면 $y_i(\textbf{w}^T\textbf{x}_i+b)= 1$, 즉 margin위에 있는 data이다. 그리고 margin위에 있지 않은 data의 경우, $\alpha_i = 0$임으로 $\textbf{w}$의 결정에 아무런 영향을 주지 않는다.
이러한 $\alpha_i \neq 0$인, margin위에 있는 data들을 Support Vector라고 한다. 그리고 Support Vector만 $\textbf{w}$에 영향을 준다. 따라서 Solution을 구할 때 모든 data를 계산할 필요 없이 Support Vector만 고려하면 된다.
$$\textbf{w} = \sum_{i=1}^N \alpha_iy_ix_i = \sum_{i\in SV} \alpha_iy_ix_i $$
- $b$
$y_i(\textbf{w}^T\textbf{x}_i+b)-1= 0$에 support vector를 대입하면 $b$를 구할 수 있다.
이론적으로 모든 support vector에 대하여 $b$는 동일한 값이 계산되어야 한다. 하지만 실질적으로 컴퓨터 상에서 계산될 때 Floating point error나 Rounding error에 의해서 조금씩 다른 값이 나온다. 때문에 일반적으로 모든 support vector로 구한 $b$의 값을 평균하여 사용한다.
- Margin
Support vector는 marginal hyperplane(위 그림의 plus/minus plane)상에 존재함으로,항상 $\textbf{w}^T\textbf{x}_j+b= y_j$를 만족한다. 이 식에 $\textbf{w} = \sum_{i=1}^N \alpha_iy_ix_i$를 대입해 $b$에 대한 식으로 정리해보자.
$$b = y_i -\sum_{i=1}^N \alpha_iy_i(x_j,x_i)$$
위 식의 양변에 $\alpha_iy_i$를 곱하고 모든 결과를 더해보자.
$$b\sum_{i=1}^N\alpha_iy_i = \sum_{i=1}^N\alpha_iy_i^2 -\sum_{i,j=1}^N \alpha_i\alpha_jy_iy_j(x_i,x_j)$$
우리는 KKT Condition을 통해 $\sum_{i=1}^N \alpha_iy_i = 0$이라는 사실을 알고있다. 그리고 $y_i$는 1이거나 -1임으로 $y_i^2 = 1$이다. 정리하면,
$$0 = \sum_{i=1}^N\alpha_i -\sum_{i,j=1}^N \alpha_i\alpha_jy_iy_j(x_i,x_j)$$
$$(\sum_{i,j=1}^N \alpha_i\alpha_jy_iy_j(x_i,x_j)= \textbf{w}^T\textbf{w})$$
$$0 = \sum_{i=1}^N\alpha_i -\textbf{w}^T\textbf{w}\;\;\;\;\Rightarrow\;\;\;\;\textbf{w}^T\textbf{w}=\sum_{i=1}^N\alpha_i$$
위에서 정의한 margin ($\rho$)에 식을 살펴보면$\rho^2 = \frac{1}{||\textbf{w}||_2^2}$이다. $\textbf{w}$에 위의 식을 대입하자.
$$\rho^2 = \frac{1}{||\textbf{w}||_2^2} = \frac{1}{\sum_{i=1}^N\alpha_i} = \frac{1}{||\alpha||_1}$$
우리는 Lagrangian multiplier를 통해 margin을 계산할 수 있다.
※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 참고하여 작성되었습니다.
댓글
댓글 쓰기