Kernel based Learning : Theoretical Foundation

-
02_1 : Kernel based Learning : Theoretical Foundation

이번 글에서는 Kernel 기반 알고리즘의 이해를 위해 기본적으로 필요한 개념을 공부해 볼 것이다.

Shatter

"A set of points is said to be shattered by a class of functions if, no matter how we assign a binary label to each points, a member of the class can perfectly separate them."

위의 정의를 살펴보면, 개별적인 각각의 point에 대하여 가능한 모든 binary label을 할당 하였을때 어떤 함수 F를 사용해 모든 point의 구분이 가능하다면, 이 point들의 집합을 Shatter 되었다 고 한다.

어떤 직선 분류기(linear classifier)가 있고, 직선 분류기에 의해 구분되는 Class를 +1, -1라고 생각하자.
그렇다면 이러한 직선 분류기를 사용하여 한 점을 +1, -1로 표현 가능하다.
그렇다면 직선 분류기를 사용하여 두 점의 모든 경우를 표현할 수 있을까?
다음과 같이 4개의 직선 분류기를 사용하면 각 직선 분류기가 각각의 A, B 두 점의 경우의 수를 표현한다. 따라서 모든 경우의 수를 표현 가능하다.

이처럼 함수 F에 대하여 n개의 point를 임의의 +1, -1을 Target value로 하는 분류 경계면의 생성이 가능하면, 함수 F가 n개의 point를 Shatter 할 수 있다고 한다.

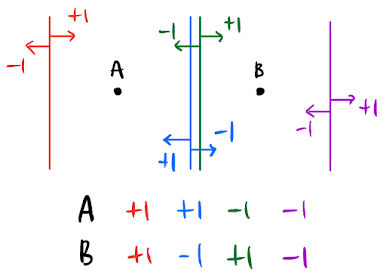
2차원 상의 점 3개도 직선 분류기를 사용하여 모든 경우의 수($2^3 = 8$가지)를 표현 가능하다.
그렇다면 2차원 상에서 점 4개를 직선 분류기를 사용하여 모든 경우의 수($2^4 = 16$가지)를 표현 가능할까?
14개의 경우를 표현 가능하지만, 우측 하단의 두 경우를 표현하지 못한다. (이 두 경우는 XOR 문제라고도 불린다)

직선 분류기는 각 차원마다 최대 몇개의 점을 Shatter 가능할까?
1차원에서 직선 분류기는 최대 2개의 점을 Shatter 가능하고,
2차원에서 직선 분류기는 최대 3개의 점을 Shatter 가능하다.
일반화 하면
N차원에서 직선 분류기는 최대 (N+1)개의 점을 Shatter 가능하다.

어떤 점들이 주어졌을 때 특정 함수 F가 해당 점들이 가질 수 있는 모든 binary classification 조합을 생성할 수 있다면 Shatter할 수 있다는 뜻이다.


Vapnik-Chervonekis Dimension (VC dimension)

H라는 분류기에 의해서 최대로 Shatter 될 수 있는 point의 수를 VC dimension이라고 한다.
VC dimension은 분류기의 Capacity(역량/복잡도)를 측정하는 지표이다. Capacity는 expressive power, richness, flexibility라고 불리기도 한다.

예를들어 2차원상에서 직선 분류기는 최대 3개의 점을 Shatter 가능하고, VC dimension은 3이다. 그렇다면 N 차원상에서 직선 분류기의 VC dimension은 (N+1)일 것이다.


Structural Risk Minimization (SRM : 구조적 위험 최소화)

구조적 위험 최소화 이론은 Machine Learning 분야에서 의심의 여지없이 가장 중요하게 여겼던 이론이다.
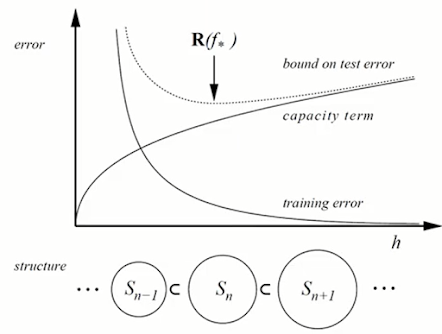
모델의 복잡도($h$)가 증가할수록 Capacity(Flexibility)는 지수적으로 증가하고, Training Error는 지수적으로 감소한다.

Capacity(Flexibility)가 증가할수록 Training data의 noise를 학습해서 일반화가 아니라 각 경우를 모두 외워버리는 상황이 생길 수 있다. 때문에 복잡도가 너무 커진다면 일반화가 잘 되지 않게되고, 점점 Test error가 증가하는(성능이 낮아지는) 상황이 발생한다. 

따라서 Training error와 Capacity의 trade-off를 고려하여 test error의 bound에 따라 bound가 가장 작은 모델을 사용하는 것이 가장 좋다는 이론이 구조적 위험 최소화이다.

다시말해 Quality of fitting the training data(empirical/training error)와 Hypothesis space Complexity(VC dimension/Capacity)의 Trade-off를 고려해서 모델의 위험을 최소화 하는(Test error bound가 가장 작은) 모델을 선택해야 한다는 이론이다.

이론을 증명하는 과정이 매우 복잡함으로 생략하고 결론을 살펴보자.

Let $h$ denote the VC dimension of the function class F and let $R_{emp}$ be defined as follows using the 0/1 loss.
$$R_{emp}[f] = \frac{1}{n}\sum_{i=1}^{n} L(f(x_i),\,y_i)$$
For all $\delta >0$ and $f \in F$ the inequality bounding the risk below holds with probability of at least $1-\delta$ for $n>h$.
$$R[f] \leq R_{emp}[f] + \sqrt{\frac{h(ln\frac{2n}{h}+1)-ln(\frac{\delta}{4})}{n}}$$

내용이 어려워 보인다. 하나씩 분석해보자.
$h$는 어떤 함수 F의 VC dimension이다. 그리고 $R_{emp}$는 구조적 위험 개념과 반대되는 경험적 위험(Empirical loss)를 뜻하는데, $x_i$에 대해서 $f(x_i)$가 정답 $y_i$와 같다면 0을 반환하고, 틀리다면 1을 반환하는 0/1 Loss function L을 사용한다. 모델 $f$에 대하여 모든 $x_i$에 대한 Loss를 구하고 이를 평균낸 것이 Empirical loss $R_{emp}$이다.
$$R_{emp}[f] = \frac{1}{n}\sum_{i=1}^{n} L(f(x_i),\,y_i)$$
그렇다면 구조적 위험 $R[f]$는 아래의 수식으로 표현된다.
$$R[f] \leq R_{emp}[f] + \sqrt{\frac{h(ln\frac{2n}{h}+1)-ln(\frac{\delta}{4})}{n}}$$
구조적 위험 $R[f]$는 우측 식에 의해서 Bound 된다는 것이 결론이다.
우측 항의 첫번째 Term은 위에서 구한 경험적 위험 $R_{emp}[f]$이다. 두번째 Capacity Term을 살펴보자.
  • $n$ : 학습 데이터의 수
  • $\delta$ : 0~1사이 확률적인 값을 나타내는 parameter
  • $h$ : 모델 $f$의 VC dimension
경험적 위험 $R_{emp}[f]$이 동일하단 가정 하에서, $n$이 증가한다면 $\frac{\log n}{n}$의 꼴 임으로 Capacity term은 감소할 것이다. 즉 학습 데이터의 수가 증가하면 구조적 위험이 감소한다. 이것은 굉장히 직관적이다. 다음 $h$를 고려해보자.

경험적 위험 $R_{emp}[f]$이 동일하단 가정 하에서, $h$가 증가한다면 $\frac{h}{\log h}$의 꼴 임으로 Capacity term은 증가할 것이다. 즉 VC dimension이 증가한다면, 구조적 위험이 증가한다.

모델의 VC dimension과 학습데이터의 수 $n$을 알고 있으니, 위의 식에서 $R_{emp}[f]$와 Capacity term을 적절히 조절하여 구조적 위험이 최소인 model을 선택하자는 것이 이 이론의 핵심이다.


Structural Risk Minimization (SRM : 구조적 위험 최소화) (Cont.)

딥러닝 기술이 엄청난 성과를 보이기 이전까지 구조적 최소화 이론은 의심의 여지 없이 받아들여지던 ML 학계의 정설이었다. 그런데 Deep Neural Network 구조에서 이 이론과 맞지 않는 결과가 나타났다.
데이터의 수보다 model parameter의 수가 몇십, 몇천배 더 많은 Deep Neural Network 모델은 구조적 위험 최소화 이론에 따르면 Capacity term이 매우 큼으로, 좋은 성능을 기대하기 어렵다. 하지만 현실에서 Deep Neural Network 모델에서 Over fitting을 적절히 control 해주면 매우 좋은 성능을 보인 것이다. 

통계학에서 가장 기본적인 상식으로 여기던 것은 Parameter의 개수보다 Training sample의 개수가 적어도 더 많아야 한다는 생각이었다. 그런데 ResNet의 결과 자료를 살펴보면,
Parameter의 개수보다 Training sample의 개수가 더 적은데도, Parameter의 개수가 179배나 더 많은데도, 적절한 처리를 수행했더니 매우 좋은 성능을 보인다는 결과가 나온다.

아직까지도 왜 DNN의 구조가 구조적 위험 최소화 이론에 맞지 않는 높은 성능이 나오는지 수학적 이론적인 완벽한 증명이 이루어지지 않았고 활발히 연구가 진행되고 있다.




※ 이 글은 고려대학교 산업경영공학과 강필성 교수님의 IME654 강의를 참고하여 작성되었습니다.




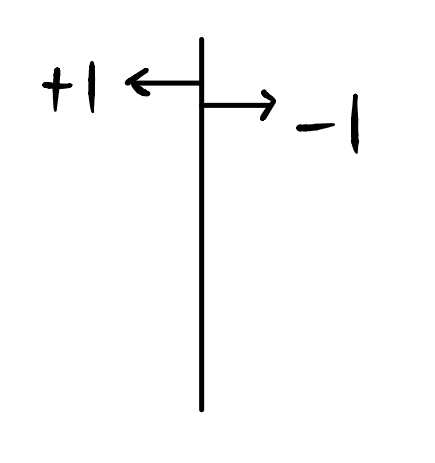
댓글

댓글 쓰기

이 블로그의 인기 게시물

One-Class SVM & SVDD

-
이미지
03_6 : Anomaly Detection : Auto-Encoder, 1-SVM, SVDD MoG와 같은 밀도기반 방법론들은 특정 객체가 정상범주에 속할 확률을 구했다. 반면 Support vector 기반 방법론들은 normal과 abnormal을 구분하는 분류경계면을 찾는다. 이번 글에서는 Support vector 기반의 Anomaly detection 방법 중 one-class SVM과 SVDD를 알아보자. One-class Support Vector Machine (1-SVM, OCSVM) 1-SVM의 목표는 Data를 feature space로 mapping 한 뒤, 분류경계면을 통해 mapping된 Data 중 normal data들이 원점으로부터 최대한 멀어지게 만드는 것이다. 위 그림에서 파란색 분류경계면이 (+1) normal data들을 구분하는 것을 확인할 수 있다. 이 목표를 수식화 한 Optimization problem부터 살펴보자. Optimization Problem $$\min_{\textbf{w}}\;\;\;\frac{1}{2}||\textbf{w}||^2 + \frac{1}{\nu l} \sum_{i=1}^l \xi_i - \rho$$ $$s.t.\;\;\;\textbf{w}\cdot \Phi (x_i) \geq \rho - \xi_i\;\;\;\;(i=1,2,\cdots,l),\;\;\xi_i\geq 0$$ $\frac{1}{2}||\textbf{w}||^2$ term은 SVR과 같이 $x$의 변화에 따른 변동이 크지 않도록 Regularization을 하는 term이다. $\rho$는 위 그림에서 주황 직선을 나타내는데, 원점과 분류경계면 Hyperplane과의 거리를 나타낸다. 이 값을 뺌으로써 최소화 문제를 만족하는 최적해일때 $\rho$가 최대가 되도록 한다. (원점에서 Hyperplane이 최대한 멀어지게 만든다) $\frac{1}{\nu l} \sum_{i=1}^l \xi_i$ term은 제약식에 따라 Hyp...
자세한 내용 보기

Support Vector Regression (SVR)

-
이미지
02_4 : Kernel based learning : Support Vector Regression (SVR) 앞에서 공부했던 SVM은 binary classification을 하기 위한 방법이었다. 이번 글에서 알아볼 SVR은 함수를 추정하여 연속적인 수치변수를 예측하는 회귀 방법이다.  SVR을 알아보기에 앞서 우리가 하려는 함수추정의 목적을 살펴보자. Fitting function 함수를 추정하고 싶을 때 우리의 목적은 크게 2가지로 나뉜다. Minimize an error measure (Loss function) 한마디로 error를 최소화 하여야 한다. (잘 맞춰야 한다) Function to be simple 같은 성능이라면, 함수는 최대한 단순해야 한다. 함수가 단순하다는 뜻은 아래의 조건들을 의미한다. Fewest basis functions Simplest basis functions Flatness is desirable Support Vector Regression (SVR) 위에서 살펴보았던 Loss function과 Flatness를 반영하도록 목적함수를 만들 것이다. SVR에도 여러 종류가 있는데, 우선 $\varepsilon$-SVR에 대하여 알아보자. 현실의 Data들은 어쩔 수 없이 발생하는 noise가 존재한다. 아래 식에서 noise는 $\varepsilon$이다. $$y = f(x)+\varepsilon$$ $\varepsilon$-SVR에서 핵심 아이디어는 $\varepsilon$ 보다 작은 noise에 대해서는 Loss를 주지 말자는 것이다.  왼쪽 그림에서 색이 칠해진 영역을 Epsilon-tube 라고 하는데, 이 영역안에 있는 객체들에게는 Loss를 부여하지 않는다. 이를 위한 Loss function은 오른쪽에 표현된다. 이 Loss function은 hinge를 닮았다고 해서, Hinge Loss 라고 불린다. 차이가 $\varepsilon$ 보다 작은 경우 loss는 0이고, $\vareps...
자세한 내용 보기

Self-Training & Co-Training

-
이미지
 05_2 : Semi-Supervised Learning : Self-Training and Co-Training 우선 가장 기본적인 준지도학습 방법 Self-Training에 대하여 알아보자.  Self-Training 우리에게 주어진 정보는 Labeled data $(\mathbf{X}_l,y_l)$과 Unlabeled data $\mathbf{X}_u$이다. Self-training과정은 다음과 같이 진행된다.  1. 우선 주어진 Labeled data $(\mathbf{X}_l,y_l)$를 사용하여 예측함수 $f$를 학습시킨다. $$y_l = f(x_l)$$ 2. 학습이 완료되면, 예측함수 $f$를 사용해 Unlabeled data $\mathbf{X}_u$의 예측값 $\hat{y}_u$를 구한다. $$\hat{y}_u = f(x_u)$$ $$\Downarrow$$ 3. 이제 기존의 Labeled data와 예측함수에 의해 labeling이 된 Unlabeled data를 합치고, 이 data를 사용해 예측함수 $g$를 학습한다. 이때 어떻게 Unlabeled data를 합치는지에 따라서 많은 variation이 있다. 대표적으로 Add all $(x_u,\hat{y}_u)$ to labeled data Add a few most confident $(x_u,\hat{y}_u)$ to labeled data Add all $(x_u,\hat{y}_u)$ to labeled data, weight each by confidence. 모든 Unlabeled data를 합치는 방법, 몇몇개의 가장 예측 confidence가 높은 data만을 합치는 방법, 모든 data를 합치치만 예측 confidence에 따라서 weight를 지정하는 방법 등이 있다. 4. 위와 같은 과정을 Unlabeled data가 없어지거나, 수렴할 때 까지 반복한다. Propagating 1-Nearest Neighbor 다른 예시로 Propagating ...
자세한 내용 보기